Задать вопрос Регистрация
Помочь другим

  • Составить рекуррентную формулу для следующего ряда. Я пробовал решать (рисунок 2), но запутался. Объясните, как составить рекуррентную формулу для данного ряда. Заранее благодарен!

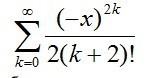
    question img
    question img

Ответы 1

  • для получения рекуррентной формулы нужно выразить член ряда через предыдущие (и, возможно, номер) a_{k+1}= \frac{ (-x)^{2(k+1)} }{2(k+3)!} = \frac{(-x)^{2k} (-x)^{2} }{2(k+2)!(k+3)} a_{k}= \frac{(-x)^{2k}}{2(k+2)!}a_{k+1}= a_{k} } \frac{ (-x)^{2} }{(k+3)} теперь возьмем член с k=1 a_{1}= \frac{ (-x)^{2} }{2*3!} отсюда (-x)^{2} = a_{1} *2*3!подставляя, получим a_{k+1}= a_{k} a_{1} \frac{2*3!}{(k+3)} это и есть рекуррентная формула

    • Автор:

      chico11
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years