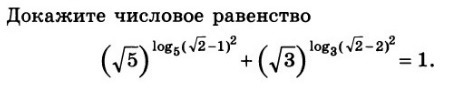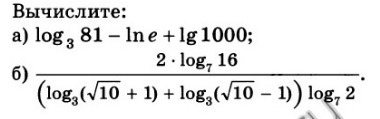Ответы 1
-
1) заметим, что 7^(㏒₂₇8) =7^(㏒₃³2³)=7^(㏒₃2) 7^(㏒₂₇8) /2^(㏒₃7) = 7^(㏒₃2) / 2^(㏒₃7) = 1т.к прологарифмируем по основанию 3 числитель : ㏒₃ 7^(㏒₃2) =㏒₃2*㏒₃7и знаменатель :㏒₃2^(㏒₃7) =㏒₃7*㏒₃2 получили ㏒₃2*㏒₃7= ㏒₃7*㏒₃2 ,что и требовалось доказать 7^(㏒₂₇8) /2^(㏒₃7)=1-----------------------------------------------------------------------------------------------------------2) (√5)^(㏒₅(√2-1)²) - (√3)^(㏒₃(√2-2)²) =5^(1/2㏒₅(√2-1)²) - 3^(1/2㏒₃(√2-2)²)=5^(㏒₅(√2-1)) - 3^(㏒₃(√2-2))= √2-1-(√2-2) = √2-1-√2+2 =1-----------------------------------------------------------------------------------------------------------------3) ㏒₃81-In е +lg1000= ㏒₃3⁴- 1 +lg10³=4-1+3=6 2*㏒₇16 2*㏒₇2⁴--------------------------------------------- = --------------------------------------- =(㏒₃( √10+1) + ㏒₃( √10-1) )*㏒₇2 (㏒₃( √10+1)*( √10-1) )*㏒₇2 2*4㏒₇2 8 8 8= ------------------------------ = --------- = ------------ = -------- = 4 (㏒₃( √10)²-1² )*㏒₇2 ㏒₃ 9 ㏒₃ 3² 2
-
Автор:
houdini - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Составь синквейн о цветах
-
Предмет:
Литература -
Автор:
moon34 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Статеве розмноження здійснюється:
а) насінням
б) спорами
в) частинами тіла -
У Вадика 70 сказок. В 3 книгах по 16 сказок. Остальные на видиокассетах по 2 скащки на каждой. Сколько видиокассет со сказками?
-
Предмет:
Математика -
Автор:
drake83 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
90 новогодних шаров разложили в 30 одинаковых коробок.Сколько шаров в 10 таких коробках?
-
Предмет:
Математика -
Автор:
bumpkinow4h - 5 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years