Задать вопрос Регистрация
Помочь другим

  • Помогите решить 2 и 3 задание ! Подробно с пояснениями * желательно на бумаге*

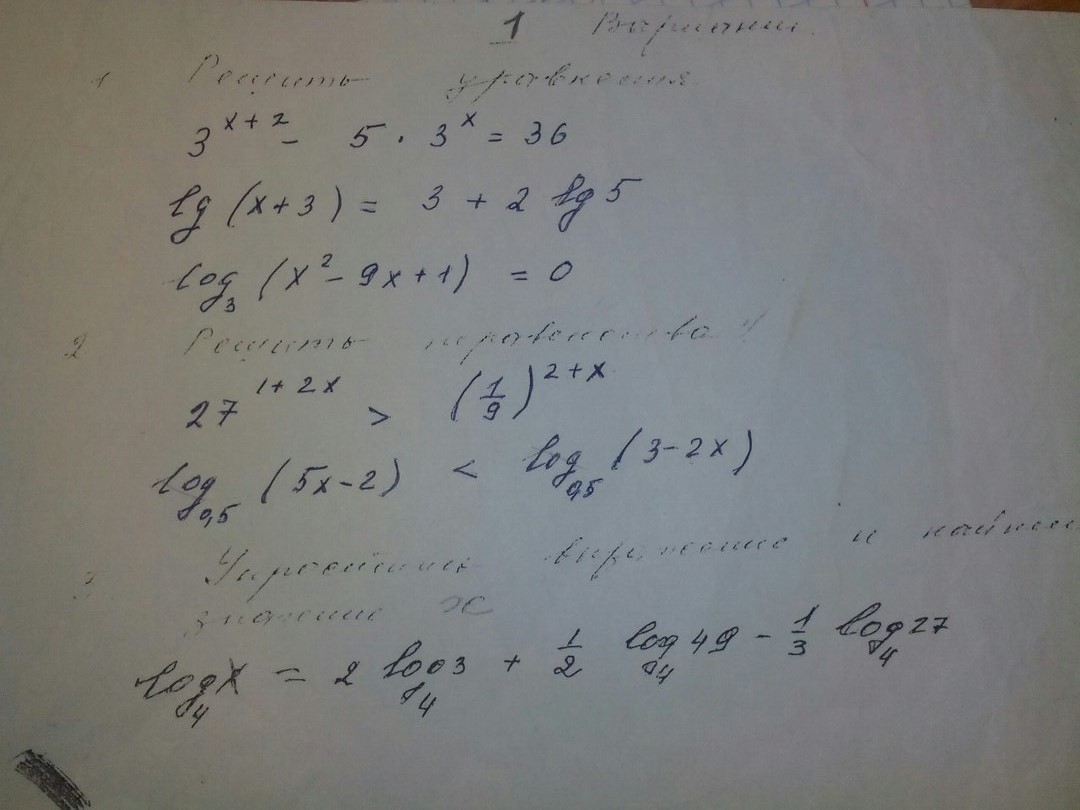
    question img

Ответы 2

  • Вам не видно ?

    • Автор:

      keiraitp9
    • 4 года назад
    • 0
  • 2)\; a)\; \; 27^{1+2x}\ \textgreater \ ( \frac{1}{9} )^{2+x}\\\\(3^3)^{1+2x}\ \textgreater \ (3^{-2})^{2+x}\\\\3^{3+6x}\ \textgreater \ 3^{-4-2x}\\\\Tak\; kak\; \; 3\ \textgreater \ 1\; ,\; to\; \; \; 3+6x\ \textgreater \ -4-2x\\\\6x+2x\ \textgreater \ -4-3\\\\8x\ \textgreater \ -7\\\\x\ \textgreater \ -\frac{7}{8}\\\\x\in (- \frac{7}{8};+\infty ) b)\; \; log_{0,5}(5x-2)\ \textless \ log_{0,5}(3-2x)\\\\ODZ:\; \; \left \{ {{5x-2\ \textgreater \ 0} \atop {3-2x\ \textgreater \ 0}} ight. \; \left \{ {{x\ \textgreater \ \frac{2}{5}} \atop {x\ \textless \ \frac{3}{2}}} ight. \; \; \to \; \; \frac{2}{5}\ \textless \ x\ \textless \ \frac{3}{2}\\\\Tak\; kak\; \; \; 0,5\ \textless \ 1\; ,\; to\; :\; \; \quad 5x-2\ \textgreater \ 3-2x\\\\5x+2x\ \textgreater \ 3+2\; \; \; \to \; \; \; 7x\ \textgreater \ 5\; ,\; \; \; x\ \textgreater \ \frac{5}{7}\\\\ \left \{ {{\frac{2}{5}\ \textless \ x\ \textless \ \frac{3}{2}} \atop {x\ \textgreater \ \frac{5}{7}}} ight. \qquad ----\underbrace {(\frac{2}{5})---\overbrace {(\frac{5}{7})---(\frac{3}{2})}}---x\in (\frac{5}{7};\frac{3}{2})3)\; \; log_4x=2log_43+\frac{1}{2}log_449-\frac{1}{3}log_427\; ,\; \; \; ODZ:\; \; x\ \textgreater \ 0\\\\log_4x=log_43^2+log_4\sqrt{49}-log_4\sqrt[3]{27}\\\\log_4x=log_49+log_47-log_43\\\\log_4x=log_4\frac{9\cdot 7}{3}\\\\log_4x=log_421\\\\x=21

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years