Задать вопрос Регистрация
Помочь другим

  • Ребята , объясните как это решать ? Задали это объяснить . Заранее спасибо большое !

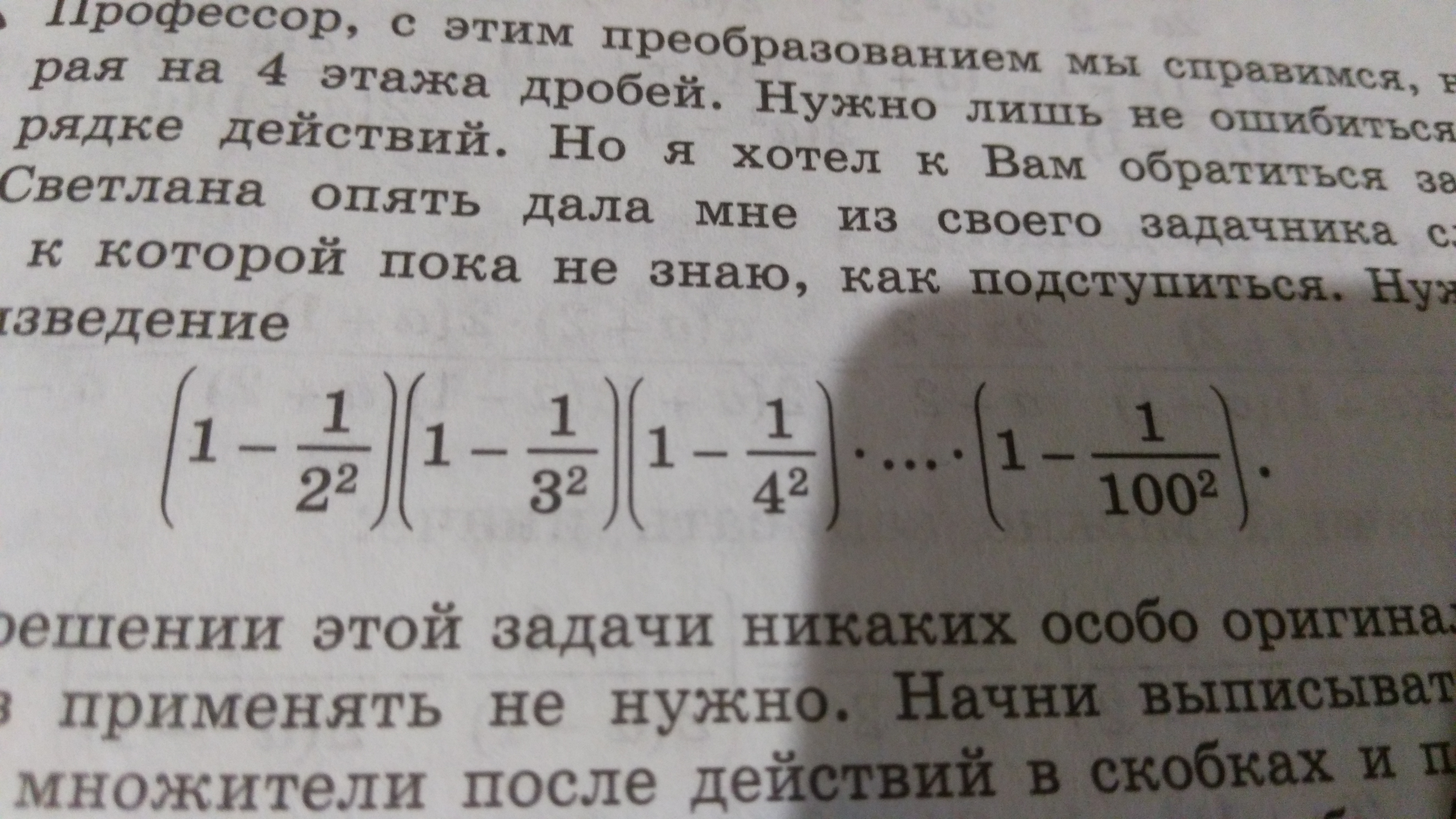
    question img

Ответы 4

  • Все слова написаны математическим текстом...

    • Автор:

      nelson
    • 5 лет назад
    • 0
  • Спасибо большое)

    • Автор:

      honorio
    • 5 лет назад
    • 0
  • В числителе и знаменателе появляются одинаковые множители, которые сокращаются и остаются только три. Как их группировать, показано в скобках.
  • (1- \frac{1}{2^2} )(1-\frac{1}{3^2})(1-\frac{1}{4^2})\cdot ...\cdot (1-\frac{1}{100^2})=\\\\= \frac{2^2-1}{2^2} \cdot \frac{3^2-1}{3^2}\cdot \frac{4^2-1}{4^2}\cdot \frac{5^2-1}{5^2} \cdot \frac{6^2-1}{6^2}\cdot ... \cdot \frac{98^2-1}{98^2}\cdot \frac{99^2-1}{99^2} \cdot \frac{100^2-1}{100^2} =\\\\= \frac{(2-1)(2+1)}{2^2}\cdot \frac{(3-1)(3+1)}{3^2} \cdot \frac{(4-1)(4+1)}{4^2}\cdot ...\cdot \frac{(98-1)(98+1)}{98^2}\cdot \frac{(99-1)(99+1)}{99^2}\cdot \\\\\cdot \frac{(100-1)(100+1)}{100^2} = = \underbrace {\frac{1\cdot 3}{2^2} \cdot \frac{2\cdot 4}{3^2}}\cdot \underbrace {\frac{3\cdot 5}{4^2}\cdot \frac{4\cdot 6}{5^2}}\cdot \frac{5\cdot 7}{6^2} \cdot ...\cdot \underbrace {\frac{96\cdot 98}{97^2} \cdot \frac{97\cdot 99}{98^2}}\cdot \underbrace {\frac{98\cdot 100}{99^2} \cdot \frac{99\cdot 101}{100^2}}== \frac{(1\cdot 2\cdot 3\cdot 4)\cdot (3\cdot 4\cdot 5\cdot 6)\cdot ...\cdot (96\cdot 97\cdot 98\cdot 99)(98\cdot 99\cdot 100\cdot 101)}{(2\cdot 3\cdot 4\cdot ...\cdot 97\cdot 98\cdot 99\cdot 100)\cdot (2\cdot 3\cdot 4\cdot ...\cdot 97\cdot 98\cdot 99\cdot 100)}== \frac{1\cdot 2\cdot (3\cdot 4\cdot 5\cdot ...\cdot 97\cdot 98\cdot 99\cdot 100)\cdot (3\cdot 4\cdot 5\cdot ...\cdot 97\cdot 98\cdot 99)\cdot 101}{2\cdot (3\cdot 4\cdot 5\cdot ...\cdot 97\cdot 98\cdot 99\cdot 100)\cdot 2\cdot (3\cdot 4\cdot 5\cdot ...\cdot 97\cdot 98\cdot 99)\cdot 100} =\\\\= \frac{101}{2\cdot 100} =0,505

    • Автор:

      tori15
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years