-
номер 269(под цифрой 3) и номер 267 (под цифрами 1 и 2)
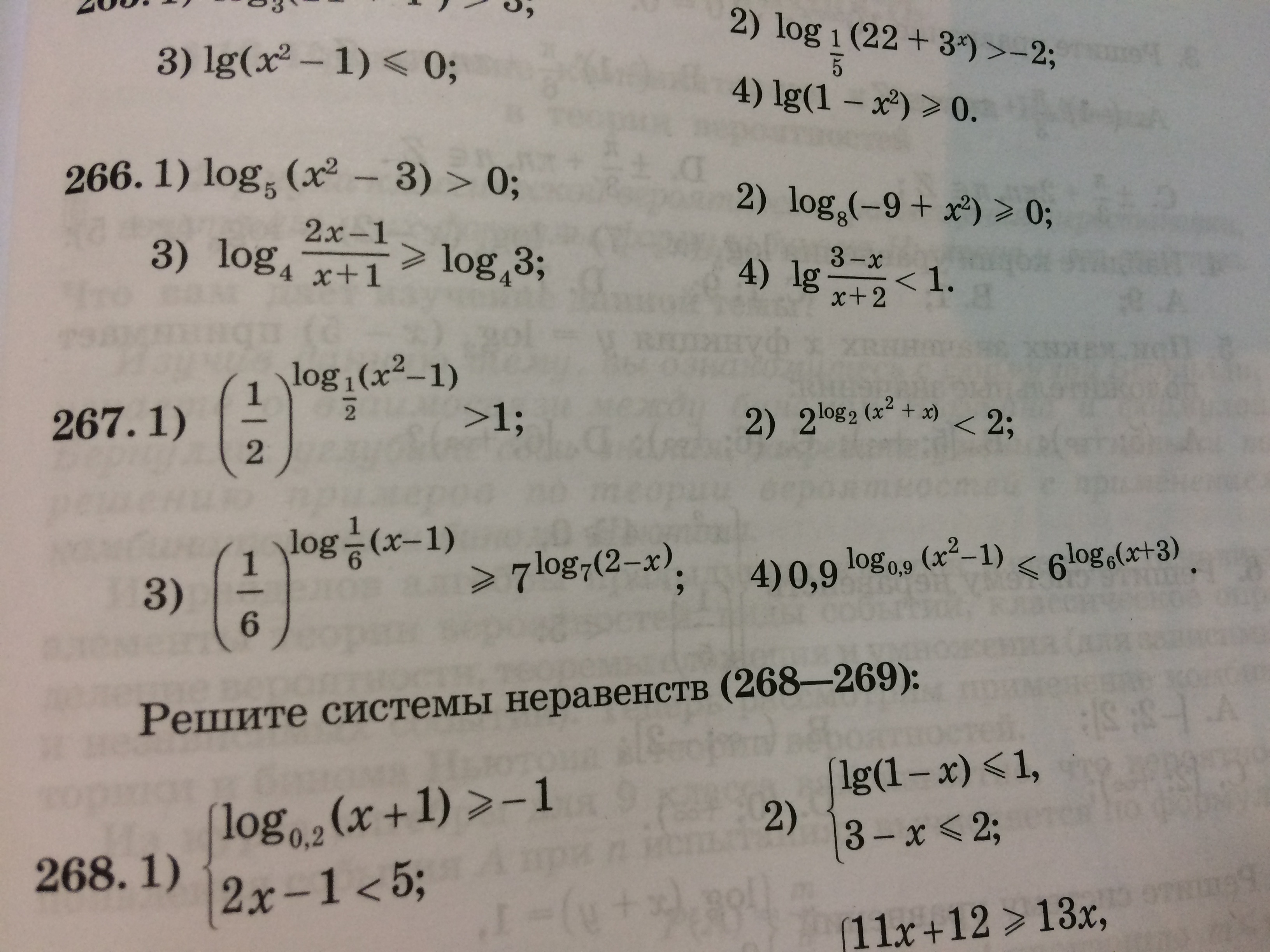
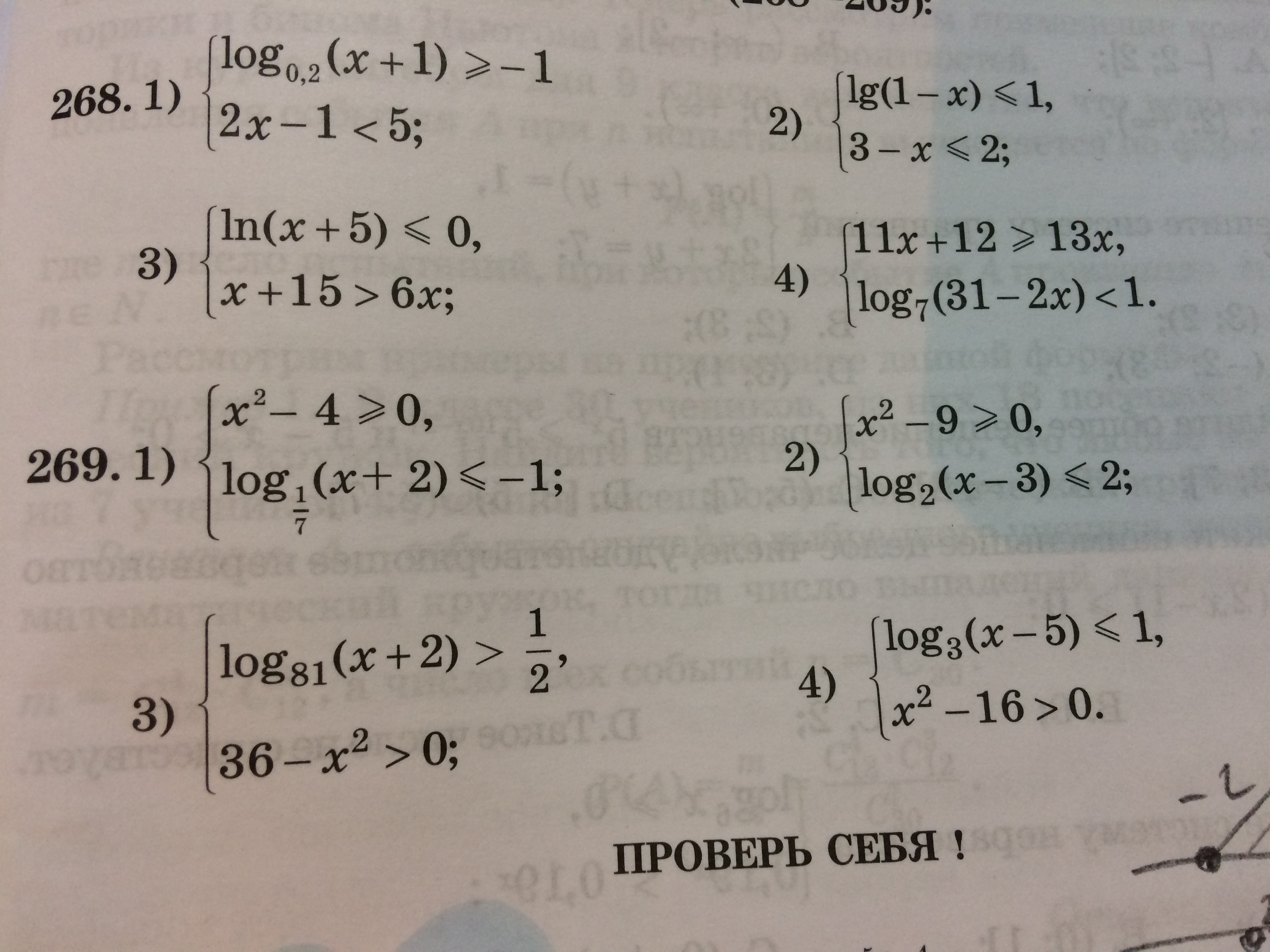
-
Предмет:
Алгебра -
Автор:
aaliyahz2ta - 5 лет назад
-
Ответы 3
-
спасибо!)
-
Автор:
gloria52 - 5 лет назад
-
0
-
-
обнови
-
Автор:
mischieftanner - 5 лет назад
-
0
-
-
#1(1/2)^(log1/2 (x^2 - 1)) > 1(1/2)^(log1/2 (x^2 - 1)) > (1/2)^0log1/2 (x^2 - 1)) < 0log1/2 (x^2 - 1)) < log 1/2 (1)x^2 - 1 > 1 x^2 > 2 x^2 - 2 > 0 (x - √2)(x + √2) > 0 ОДЗx^2 - 1> 0 (x - 1)(x + 1) > 0 x ∈ (- ∞ ; - 1) ∪ (1; + ∞) + - + --------- (- √2 ) -------------( √2) -----------------> x Ответx ∈ ( - ∞ ; - √2) ∪ (√2; + ∞)#22^(log 2(x^2 + x)) < 2^1x^2 + x - 2< 0 x ∈ ( - 2; 1)#3log81 (x + 2) > 1 /236 - x^2 > 0 (6 - x)(6 + x) > 0 log81 (x + 2) > log81 (9)(x - 6)(x + 6) < 0 x + 2 > 9x ∈ ( - 6; 6 )x ∈ (7; + ∞) + одз x > - 2нет решений ∅
-
Автор:
cheesestick6z5d - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Вырожение составить. В кинотеатре a рядов по b мест в каждом. Сколько всего мест в кинотятре.
-
Предмет:
Математика -
Автор:
chessie - 5 лет назад
-
Ответов:
0 -
Смотреть
-
- история военного знамени в разные эпохи
- Найдите косинус наименьшего угла треугольника, стороны которого равны 40 см, 70 см, 95 см.
-
Прочитай .Озаглавь стихотворение .Укажи в каком числе стоя
-
Предмет:
Русский язык -
Автор:
ethanbd5w - 5 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
