-
Решение интегралов, 11 класс
Дам лучший за полное и правильное решение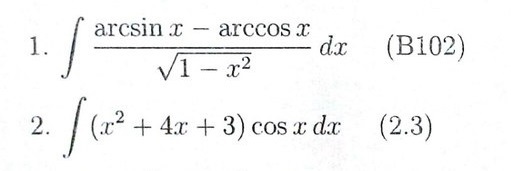
Ответы 1
-
∫(arcsinx-arccosx)/√(1-x²)dx∫arcsinx/√1-x²dx=∫arcsinxd(arcsinx)=arcsin²x/(2)∫arccosx/√1-x²dx=∫arccosxd(-arccosx)=-arccos²x/(2)исходный интеграл равен 0.5(arcsin²x+arccos²x)+C-----------------------------∫(x²+4x+3)cosxdx ∫x²cosxdx = интегрирование по частям -формула ∫fdg=fg-∫gdf f=x² dg=cosxdx df=2xdx g=sinx=x²sinx-2∫xsinxdx= cнова по частям f=x dg=sinxdx df=dx g=-cosx=x²sinx+2xcosx-2∫cosxdx=x²sinx+2xcosx-2sinx+c4∫xcosxdx=4∫xd(sinx)=4xsinx-4∫sinxdx=4xsinx+4cosx+c3∫cosxdx=3sinx+cинтеграл в целом равен x²sinx+2xcosx-2sinx+4xsinx+4cosx+3sinx
-
Автор:
quinn116 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
2,284*10^-25
____________
1,66*10^-27
(Подробно ) - У равнобедренном треугольниуе с периметром 48 см, боковая сторона относится до основы как 5:2. Найти стороны треугольника
-
каково согласно мифам,происхождение географического названия Кавказ
-
Предмет:
Другие предметы -
Автор:
cozmo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Электрическая печь,сделанная из никелиновой проволоки длинной 56,25м сечением 1.5 мм в квадрате . присоединена к сети напряжением 120 В. Определите силу тока. протекающего по спирали, ВОТ))
-
Предмет:
Физика -
Автор:
taniyahojsc - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
