-
СРОЧНО!!!! НУЖНО ПОЛНОЕ И ПОДРОБНОЕ НАХОЖДЕНИЕ ПРЕДЕЛА !! Если что ответ 3/4
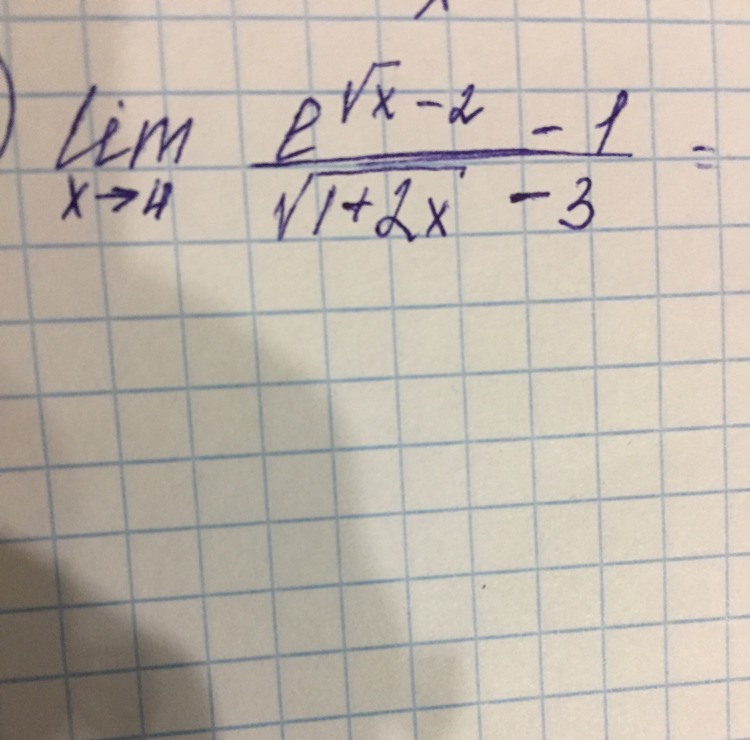
Ответы 1
-
-
Автор:
shania - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Всем привет друзья. Плиз скажите, что такое фауна и флора? Сәлем достар өтініш маған көмектесіп жіберіңіздерші. Флора мен Фауна деген не?
-
срочно сиквейн на тему мир никиты
-
Предмет:
Литература -
Автор:
mejia - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
сколько и какие натуральные значения X, при которых верно неравенство 4.36<X<10,16?
Срочняк-
Предмет:
Математика -
Автор:
sandoval - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Укажите какие из перечисленных ниже утверждений верны
1)Высота всегда образует с прямой содержащей одну сторону треугольника равные углы.
2)В прямоугольном треугольнике высота может совпадать с одной из его сторон
3)Высота всегда делит треугольник на два треугольника равной площади
4)Высота может лежать и вне треугольника
How much to ban the user?
1 hour
1 day
100 years
