-
Помогите решить задачи по тригонометрии.
Срочно
"Решите №3 задание (в)"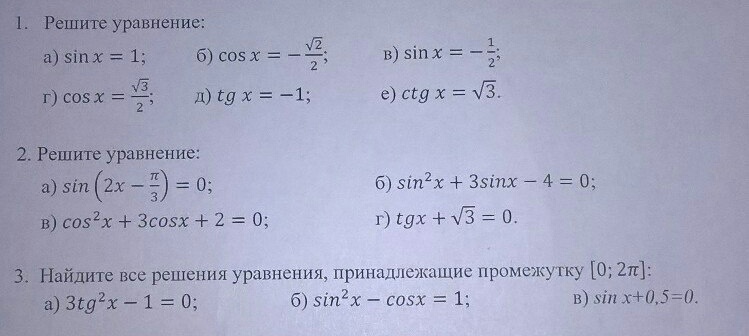
Ответы 2
-
так вроде
-
Автор:
nickolas - 5 лет назад
-
0
-
-
1.a.sinx=1x=pi/2+2pin,n∈Zb.cosx=-√2/2x=(+/-)3pi/4+2pin,n∈Zc.sinx=-1/2x=(-1)^(n+1)*pi/6+pin,n∈Zd.cosx=√3/2x=(+/-)pi/6+2pin,n∈Ze.tgx=-1x=-pi/4+pin,n∈Zf.ctgx=√3x=pi/6+pin,n∈Z2.a.sin(2x-pi/3)=0-cos(2x+pi/6)=0cos(2x+pi/6)=02x+pi/6=pi/2+pin,n∈Z2x=pi/3+pin,n∈Zx=pi/6+(pin)/2,n∈Zc.cos²x+3cosx+2=0(1+cosx)(2+cosx)=01+cosx=0 or 2+cosx=0cosx=-1 or cosx=-2 nonex=pi+2pin,n∈Zb.sin²x+3sinx-4=0(sinx-1)(4+sinx)=0sinx-1=0 or 4+sinx=0sinx=1 or sinx=-4 nonex=pi/2+2pin,n∈Zd.tgx+√3=0tgx=-√3x=-pi/3+pin,n∈Z3.a.3tg²x-1=03tg²x=1tg²x=1/3tgx=1/√3 or tgx=-1/√3x= pi/6+pin,n∈Z or x=-pi/6+pim,m∈Z[0;2pi]x1=pi/6x2=5pi/6x3=7pi/6x4=11pi/6b.sin²x-cosx=1-cos²x-cosx=0cosx(1+cosx)=0cosx=0 or 1+cosx=0cosx=0 or cosx=-1x=pi/2+pin,n∈Z or x=pi+2pim,m∈Z[0;2pi]x1=pi/2x2=pix3=3pi/2c.sinx+1/2=0sinx=-1/2x1=7pi/6+2pin,n∈Zx2=11pi/6+2pim,m∈Z[0;2pi]x1=7pi/6x2=11pi/6
-
Автор:
gay44 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Разобрать по членам предложения.
Старший приказал брату Федьке бежать во весь дух в деревню и звать народ.-
Предмет:
Русский язык -
Автор:
george97 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Воспроизведение уравнения химических рекций по приведенным фрагментам:
а)Mg+H2SO4 -->...+H2
б)Fe+...-->FeCl2+H2
в)Ni+..-->NiSO4+H2
г)MgO+H2SO4-->...+H2O
д)Li2O+HBr-->LiBr+...
e)Al+HBr-->AlBr3+..
ж)Mg+H3PO4-->...+Mg3(PO4)2-
Предмет:
Химия -
Автор:
victor7qc5 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
какая это дробь 0,00,8
-
Предмет:
Математика -
Автор:
beckett - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Сочинение
На тему:золотые руки моей бабушки
-
Предмет:
Литература -
Автор:
marisasalas - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
