-
Помогите решить неравенство, с подробным решением, пожалуйста, срочно! (
Если что, в начале тройка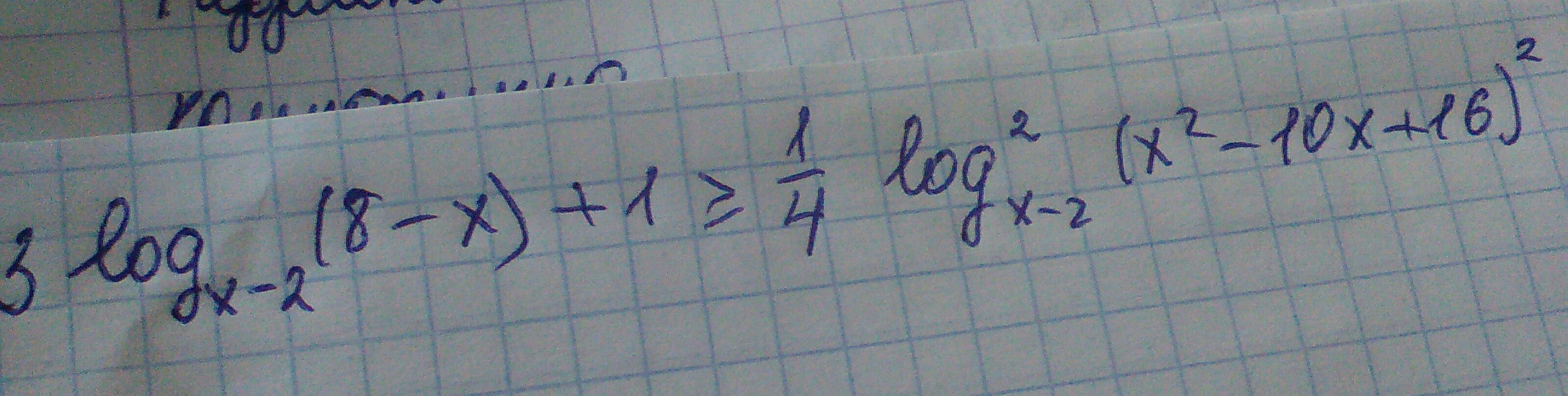
Ответы 1
-
Теперь воспользуемся теоремой о знаке логарифма, оно же метод рационализации, ....Суть метода: если логарифмы определены, то
даёт такой же знак, что и
.ОДЗ: x - 2 > 0, x - 2 ≠ 1, 8 - x > 0x ∈ (2, 3) ∪ (3, 8)На ОДЗ неравенство равносильно такому:
Получилось обычное равенство, которое легко решается методов интервалов:
Это решение, кроме 3, входит в ОДЗ, поэтому окончательный ответ такой:
-
Автор:
stanley - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Пожалуйста, помогите
Напишите пять вопросов к тексту:
1. Да либо Нет(Общий)
2.Альтернативный (... or ...?)
3.Раздельтельный (isnt it / aren't you? (не так ли?) )
4.Специальный
5.Вопрос к подлежащему
IT’S ONLY ME
After her husband had gone to work, Mrs Richards sent her children to school and went upstairs to her bedroom. She was too excited to do any housework that morning, because in the evening she would be going to a fancy dress party with her husband. She intended to dress up as a ghost and she had made her costume the night before. Now she was impatient to try it on. Though the costume consisted only of a sheet, it was very effective. Mrs Richards put it on, looked in the mirror, smiled and went downstairs. She wanted to find out whether it would be comfortable to wear.
Just as Mrs Richards was entering the dining-room, there was a knock on the front door. She knew that it must be the baker. She had told him to come straight in if ever she failed to open the door and to leave the bread on the kitchen table. Not wanting to frighten the poor man, Mrs Richards quickly hid in the small store-room under the stairs. She heard the front door open and heavy footsteps in the hall. Suddenly the door of the store-room was opened and a man entered. Mrs Richards realized that it must be the man from the Electricity Board who had come to read the meter. She tried to explain the situation, saying 'It's only me', but it was too late. The man let out a cry and jumped back several paces. When Mrs Richards walked towards him, he ran away, slamming the door behind him.
ЭТО ТОЛЬКО ДЛЯ МЕНЯ
После того, как ее муж ушел на работу, миссис Ричардс отправила своих детей в школу и пошла наверх в свою спальню. Она была слишком взволнована, чтобы делать любую работу по дому утром, вечером она должна была идти на вечеринку в платье со своим мужем. Она намеревается надеть платье наверх, как призрак, и так как она сделала свой костюм перед ночью, она была нетерпелива, чтобы попробовать надеть на себя. Хотя костюм состоял только из простыни, он был очень эффективным. После сдачи его, миссис Ричардс спустилась вниз. Она хотела бы выяснить, будет ли комфортно его носить.
Как раз, миссис Ричардс входила в столовую, и был стук входной двери. Она знала, что там должен был быть пекарь. Она сказал ему пройти в переднюю, если когда-нибудь она не сможет открыть дверь и оставить хлеб на кухонном столе. Не желая пугать бедняка, миссис Ричардс быстро спряталась в небольшой кладовке под лестницей. Она услышала, что открылась передняя дверь и тяжелый звук ног в зале. Внезапно дверь склада была открыта, и вошел мужчина. Миссис Ричардс поняла, что он должен быть человек от электричества Совета, который пришел смотреть счетчик. Она попыталась объяснить ситуацию, сказав, «Это только меня», но было слишком поздно. Мужчина прокричал и прыгнул назад, отскочив на несколько шагов. Когда миссис Ричардс направилась по направлению к нему, он побежал, хлопнув за собой дверью.-
Предмет:
Английский язык -
Автор:
alfredoclark - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Небольшой рассказ про имбирные пряники на английском языке (процесс изготовления).
-
Предмет:
Английский язык -
Автор:
nickystout - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
154800:10 на листочек
-
Предмет:
Математика -
Автор:
brittanyamtj - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
почему заключение брака в церкви называется венчание
-
Предмет:
Другие предметы -
Автор:
israel974 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
