-
Помогите пожалуйста решить системы уравнений под буквами б) и г)!!!
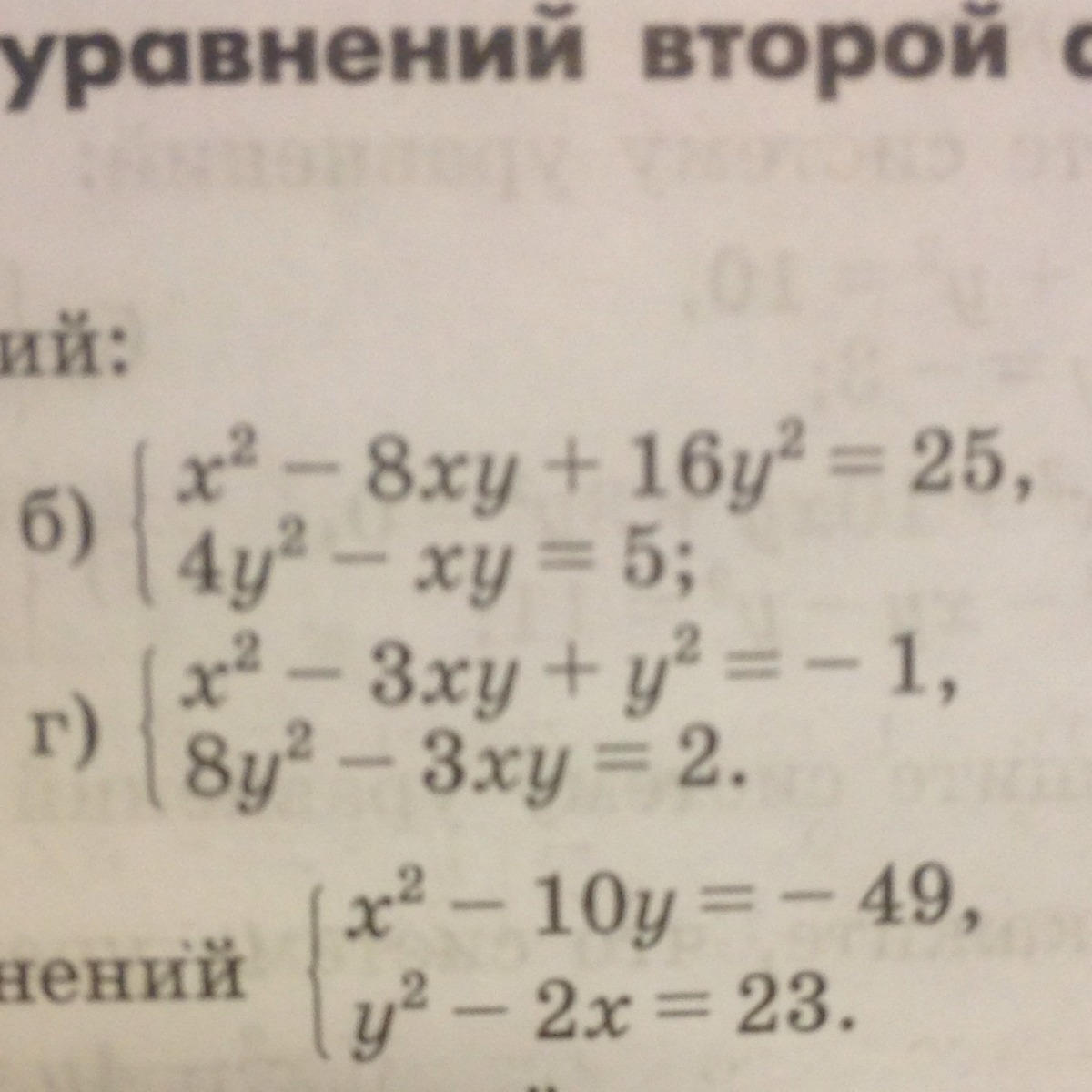
-
Предмет:
Алгебра -
Автор:
ricardomnsv - 6 лет назад
-
Ответы 1
-
б)
Распадается на 2 системы1)
Подставляем 1 уравнение во 2 уравнение, получаемy1 = 1; x1 = -5 + 4y = -5 + 4 = -1(-1; 1) - это решение.2)
Подставляем 1 уравнение во 2 уравнение, получаемy2 = -1; x2 = 5 + 4y = 5 - 4 = 1(1; -1) - это решение.Ответ: (-1; 1); (1; -1)г)
Левые части равны, значит, равны и правыеx^2 + y^2 + 1 = 8y^2 - 2x^2 + 3 = 7y^2y = √(x^2 + 3)/√73xy = 3x/√7*√(x^2 + 3) = x^2 + (x^2 + 3)/7 + 13x/√7*√(x^2 + 3) = 8/7*x^2 + 10/7Умножаем все на 73x*√7*√(x^2 + 3) = 8x^2 + 10Возводим все в квадрат9*7x^2*(x^2 + 3) = (8x^2 + 10)^263x^4 + 3*63x^2 = 64x^4 + 160x^2 + 100x^4 + 160x^2 - 189x^2 + 100 = 0x^4 - 29x^2 + 100 = 0(x^2 - 4)(x^2 - 25) = 0(x + 2)(x - 2)(x + 5)(x - 5) = 0x1 = -5; x2 = -2; x3 = 2; x4 = 5y = √(x^2 + 3)/√7 >= 0, потому что корень арифметическийy1 = √(25 + 3)/√7 = √(28/7) = √4 = 2y2 = √(4 + 3)/√7 = √7/√7 = 1y3 = y2 = 1; y4 = y1 = 2Но решения (-5; 2) и (-2; 1) не подходят к начальным уравнениям, поэтомуОтвет: (2; 1); (5; 2)
-
Автор:
meggie - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Посмотрите на фотографии этих забавных животных и сказать, кто есть кто. (по примеру)
-
Предмет:
Английский язык -
Автор:
asherandrews - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите , пожалуйста, с математикой: Чему равен корень уравнения: 0,1х+9=0,2-4
-
Предмет:
Математика -
Автор:
roryk1ok - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
слово где ть корень а потом окончание и все
-
Предмет:
Русский язык -
Автор:
wigglesj6du - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Что означает имя Геракл?
Помогите пожалуйста-
Предмет:
Литература -
Автор:
bernardolong - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
