-
Решите неравенство, применяя теоремы о равносильности неравенств:
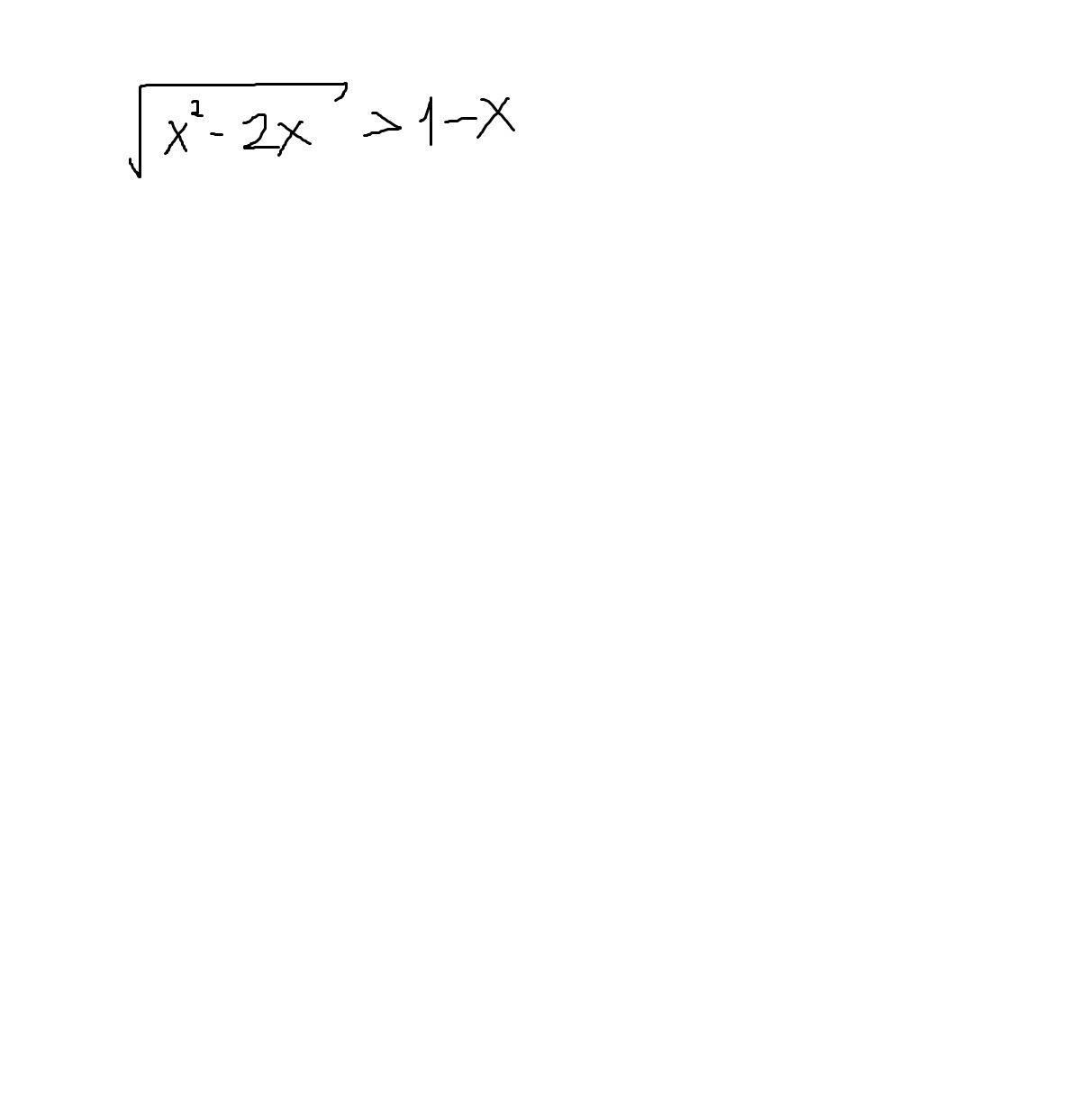
-
Предмет:
Алгебра -
Автор:
kirahanson - 5 лет назад
-
Ответы 1
-
Неравенство равносильно совокупности двух систем:
и
Решаем первую систему:
Решаем вторую систему:
Второе неравенство неверно, значит вся система не имеет решений.Тогда общее решение совокупности совпадает с решением первой системы:
Ответ:
-
Автор:
izayah - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Найдите площадь равнобедренного треугольника АВС, если АВ=ВС=10 см, а угол В равен 30 градусов.
-
НАЙТИ ЗНАЧЕНИ ВЫРАЖЕНИЕ СРОЧНО! 2/3+ 6 3/7 - 2/21 ПОМОГИТЕ!(
-
Предмет:
Математика -
Автор:
rubiozm95 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Пересказ А.П.Платонов Любовь к родине или путишествие воробья
Если я это не зделала мне поставят 2 помогите пожалуйста-
Предмет:
Литература -
Автор:
duke8rku - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
У мамы было 1350 рублей.На покупки мама истратила 540 рублей.Сколько процентов денег осталось
-
Предмет:
Математика -
Автор:
gwendolynbradford - 5 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
