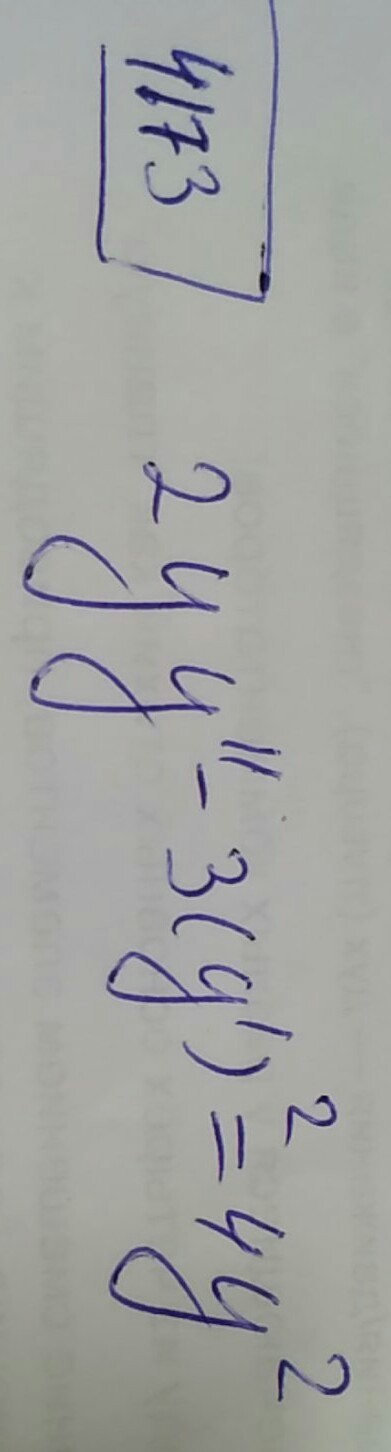Ответы 1
-
Это дифференциальное уравнение второго порядка независящее явным образом от независимой переменной х.Понизим порядок производной.Пусть y' = p(y), тогда y'' = p*p'(y). Имеем:
Пусть l = p², тогда
Получили дифференциальное уравнение первого порядка, линейное неоднородное.Пусть
тогда
Данное решение состоит из двух этапов:1) Предполагаем, что второе слагаемое равен нулю:
Интегрируя обе части уравнения, получаем:
2) Второе слагаемое равен нулю, значит
Снова интегрируя, получаем:
Обратная замена:
-
Автор:
mountaini8ib - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
5 предложений про казанские достопримечательности НА ТАТАРСКОМ!
-
Предмет:
Другие предметы -
Автор:
wrigleyk5go - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
реши уравнение с-(62-47)=39
-
Предмет:
Математика -
Автор:
natashaxix2 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
найти острые углы треугольника ABC
помогите пж -
СРОЧНО,ОТВЕТЬТЕ ПОЖАЛУЙСТА (ЗАРАНЕЕ СПАСИБО):1.В процессе дыхания:
А)органические вещества передвигаются из клетки в клетку
Б) образуются сложные вещества из более простых
В) происходит расщепление органических веществ с выделением энергии
2.К белкам относятся:
А) гемоглобин Б)крахмал
В) клетчатка Г)соли натрия
3.Хлоропласты есть в клетках:
А)лука Б)гусеницы бабочки
В)стебеля моркови Г)бактерии ,вызывающей туберкулез
4.У обыкновенной амёбы:
А) есть образовательные ткани Б)есть покровная ткань
в) есть соединительная ткань Г)нет тканей
5.К органам пищеварительной системы относят:
А)трахею Б)желудок
В)почки В)иглы
6.Отдельным органом можно считать:
А)лепестки цветка люпина Б)корень томата
В)хлоропласты клеток листа фасоли Г)древесину сосны
7.С помощью кровеносной системы в организме животного осуществляется перенос :
А) кислорода Б)веществ,которые нужно удалить из организма
В)питательных веществ Г)всего выше перечисленного
8.Переваривание пищи у дождевого червя происходит:
А)внутри клеток Б)внутри организма, но вне клеток
В)вне организма Г)бывает по разному
9.Поступление углекислого газа внутрь листа обеспечивает :
А)жилки листа Б)устьица
В)чечевички Г)прозрачные клетки кожицы листа
10.Целостность строения организма обеспечивает:
А) сложное строение Б) взаимосвязь тканей и органов
В)взаимосвязь организма и среды Д) способность к дыханию.
-
Предмет:
Биология -
Автор:
estherscze - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years