-
Научите пожалуйста решать такие уравнения, нудны действия по порядку, а то не знаю, как такие решать
Под буквой А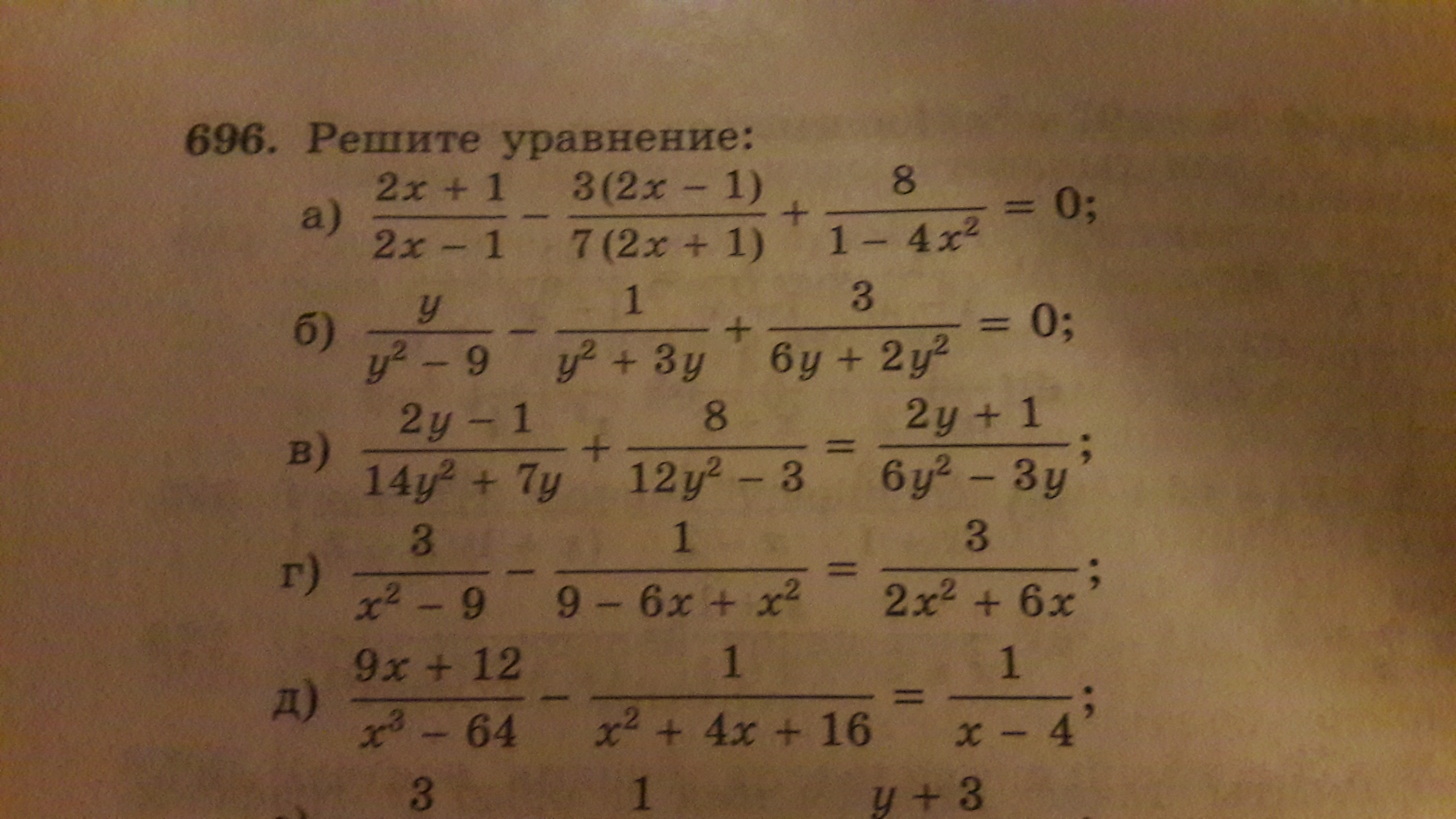
-
Предмет:
Алгебра -
Автор:
sánchezbcxk - 5 лет назад
-
Ответы 1
-
(2х+1)/(2х-1) - 3(2х-1)/7(2х+1) + 8/(1-4х^2) = 0(2х+1)/(2х-1) - 3(2х-1)/7(2х+1) - 8/(4х^2 - 1) = 01) В знаменателе третьей дроби:4х^2 - 1 = (2х-1)(2х+1)2) Умножим обе части уравнения на 7(2х+1)(2х-1), чтобы избавиться от знаменателей:7(2х+1)^2 - 3(2х-1)^2 - 8•7 = 03) Раскроем скобки:7•4х^2 + 7•4х + 7•1 -3•4х^2 + 3•4х - 3•1 - 56 = 028х^2 + 28х + 7 - 12х^2 + 12х - 3 - 56 = 04) Приведем подобные члены:16х^2 + 40х - 52 = 05) Сократим обе чести уравнения на 4:4х^2 + 10 х - 13 = 06) Дискриминант D = 10^2 -4•4•(-13) = 100 + 208 = 3086) √D = √308 = 2√777) х1 = (-10 - 2√77)/2•4 = -(5 + √77)/4х2 = (-10 + 2√77)/2•4 = -(5 - √77)/4
-
Автор:
esdras - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Укажи цифрами транспортное средство, последовательно отвечая на вопросы.
1. Самосвал 2. Дельтоплан 3. Автобус 4. Парашют 5. Трамвай 6. Велосипед
7. Лыжи 8. Аэробус
Личный транспорт
Да Нет
Да зимний грузой Да
Нет Нет
Да наземный воздушный Да
Нет Нет
Да двигатель есть? Рельсовый Да
Нет Нет
-
Предмет:
Окружающий мир -
Автор:
ashtynriddle - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста.
На рисунке. BD параллельна AC,BO=OD. Докажите,что AB=AD,BC=CD. Найдите угол OBC,если угол ODC=65 градусов. -
Яка в середньому площа лісу припадає на одну людину на планеті ,якщо його запаси становлять 3,5 млрд.га?
а) 0,5 га/ос.
б) 1,5 га/ос.
д) 2,5 га/ос.
б) 1 га/ос.
г) 2 га /ос. -
Раскройте скобки, употребляя глаголы в одном из следующих времен: Present continuous ,Present Simple ,Past simple ,future simple .
1)various kinds of sports (to be) popular in Russia.2) Both children and grown-ups (to be) ford of sports .3)What (to be) the matter with her?She (to be) so excited .- I (not to know).4)Where you (to go) ?- I(to go) to the stadium to see the match which (to take) place there today .5)You (to know) that a very interesting match (to take) place last sunday?6) He (to go) to the south a week ago.7)When I(to be)about fifteen years old ,I (to enjoy) playing football.8)our football team (to win) many games last year.9)Where Boris (to be)?-He (to play) chess with his friend.10)I (to be)sorry i (to miss) the match yesterday.But I(to know)the score .It (to be) 4 to 2 in favour of the Russian team.I (to be) absolutely happy.11) I (to think) Nellie (to leave) for Moscow tomorrow.12) I (to be) in a hurry . My friends (to wait) for me .13) You (to be)at the theatre yesterday .You (to like)the opera?- Oh yes ,i(to enjoy) it greatly .14)we (to expect) you (to go) to london next summer. 15)Her english (not to be) excellent ,but she (to work) on it .16) A week ago they (not to know) what to think.17) she (to worry)a lot at the moment but the problems (not to be)very great .18)Last tuesday he (to be)upset and (to have) no idea where to go .19)Could you tell me the way to trafalgar square? I (to go)the right way.-
Предмет:
Английский язык -
Автор:
jorge9l64 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
