Задать вопрос Регистрация
Помочь другим

  • Логарифмы. Можете пожалуйста решить, что сможете! Буду благодарен

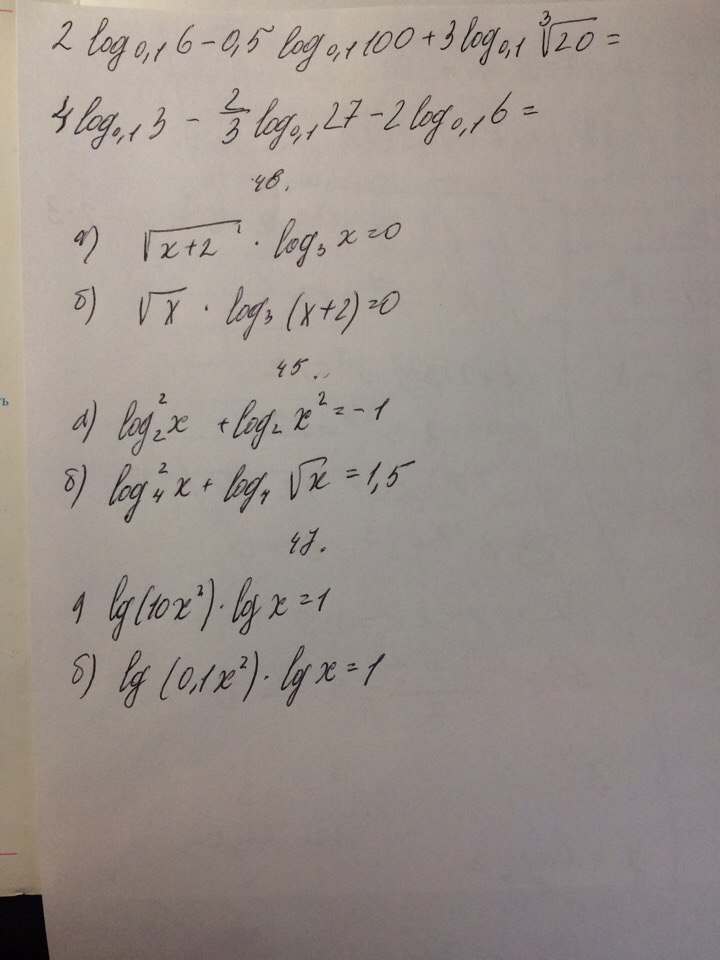
    question img

Ответы 1

  • 1) 2log_{0,1}(6)-log_{0,1}(100)+3log_{0,1} \sqrt[3]{20} =log_{0,1}( \frac{6^2}{100}*( \sqrt[3]{20} )^3 )==log_{0,1}( \frac{36*20}{100} )=log_{0,1}( \frac{36}{5} )=log_{0,1}(7,2)=-lg(7,2)2) 4log_{0,1}(3)-2/3*log_{0,1}(27)-2log_{0,1}(6)=log_{0,1} (\frac{3^4}{ \sqrt[3]{27^2}*6^2 } )==log_{0,1}( \frac{81}{9*36} )=log_{0,1}( \frac{81}{9*9*4} )=log_{0,1}( \frac{1}{4} )=-lg( \frac{1}{4} )=lg(4)46. а)  \sqrt{x+2}*log_3(x)=0 Область определения x > 0, поэтому x = -2 не подходит.x = 1; log_3(1)=0б) \sqrt{x}*log_3(x+2)=0Область определения x > -2, поэтомуx1 = 0; x + 2 = 1; x2 = -145. а) log_2^2(x)+log_2(x^2)=-1log_2^2(x)+2log_2(x)+1=(log_2(x)+1)^2=0log_2(x)=-1; x=2^{-1}=1/2x = 1/2б) log_4^2(x)+log_4( \sqrt{x} )=1,5log_4^2(x)+0,5log_4( x)-1,5=0,5(log_4( x)-1)(2log_4( x)+3)=0log_4(x)=1; x1=4log_4(x)=-3/2;x2=4^{-3/2}= \frac{1}{4^{3/2}} = \frac{1}{2^3} = 1/8x1 = 4; x2 = 1/847. а) lg(10x^2)*lg(x)=1(lg(10)+lg(x^2))*lg(x)=(1+2lg(x))*lg(x)=12lg^2(x)+lg(x)-1=(lg(x)+1)(2lg(x)-1)=0lg x = -1; x1 = 0,1; lg x = 1/2; x2 = 10^(1/2) = √10Ответ: x1 = 0,1; x2 = √10б) lg(0,1x^2)*lg(x)=1(lg(0,1)+lg(x^2))*lg(x)=(-1+2lg(x))*lg(x)=12lg^2(x)-lg(x)-1=(lg(x)-1)(2lg(x)+1)=0lg x = 1; x1 = 10; lg x = -1/2; x2 = 10^(-1/2) = 1/10^(1/2) = 1/√10Ответ: x1 = 10; x2 = √10/10Всё!

    • Автор:

      mooseeiqs
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years