-
ПОМОГИТЕ С ЛОГАРИФМАМИ
Желательно бы решить первый и второй
Очень надеюсь на вашу помощь:(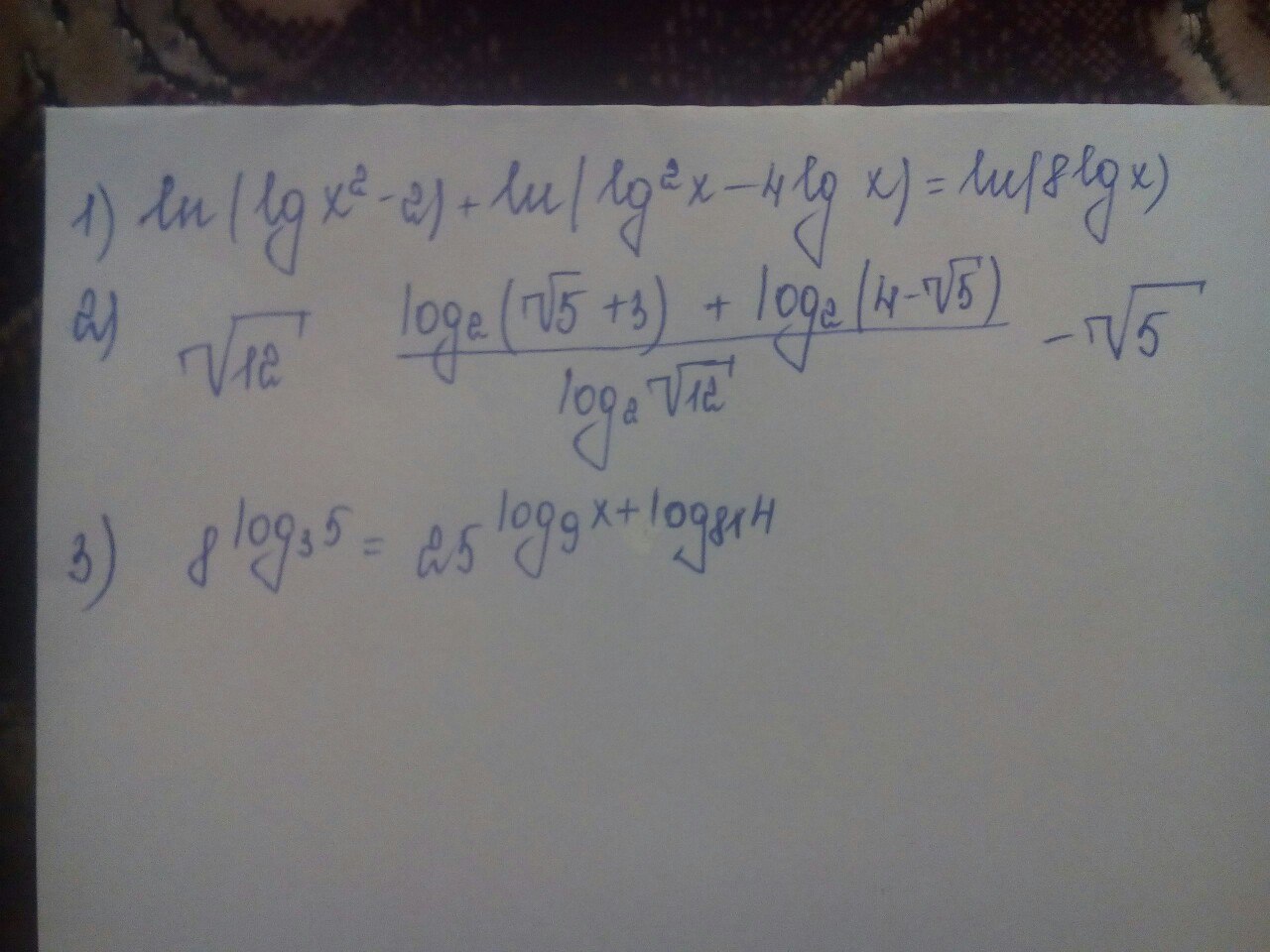
Ответы 1
-
-
Автор:
hollymueller - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогиите пожал!!!!Наити синонимы к словам запах и темноте
-
Предмет:
Русский язык -
Автор:
boo53 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
В каких словах звуков больше чем букв:
1) объеденный, 2)циркуль, 3)мельник, 4)тесьма, 5)старенькая, 6)голубь.-
Предмет:
Русский язык -
Автор:
diaz8 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- Помогите пожалуйста! Очень надо, никогда не дружил с геометрией.
-
решите пожалуйста этот вопрос
очень срочно нужно ✍-
Предмет:
Математика -
Автор:
raymond242 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
