-
Найти наибольшее значение функции y=sin^2(2x) / sin^4(x)+cos^4(x)
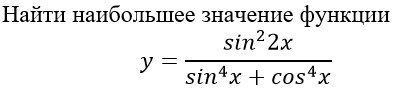
-
Предмет:
Алгебра -
Автор:
geraldzd9j - 5 лет назад
-
Ответы 2
-
спасибо за проделанную работу
-
Автор:
amiracannon - 5 лет назад
-
0
-
-
В точке экстремума y' = 0.
sin 4x = 04x = πn, n ∈ Zx = πn/4, n ∈ ZСреди этих экстремумов максимумы: x = π/4 + πn/2, n ∈ Z.Максимальное значение функции:
-
Автор:
alfmartin - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Сочинение на английском на тему осень
-
Предмет:
Английский язык -
Автор:
cassie - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
В гараже находилась 340 автомашин трёх видов автомашину москвич составляли 45 % от числа машину жигули а число автомашины запорожец составляла пять девятых от числа автомашину москвич сколько автомашин каждого вида находилась в гараже
-
Предмет:
Математика -
Автор:
azkaban - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
в 1к-? на 0,2 кг меньше чем во 2к всего 13,16кг яг.
-
Предмет:
Математика -
Автор:
regan - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
ПОЖАЛУЙСТА,ПОМОГИТЕ,СРОЧНО НАДО!!!
1. Subdivide the following words of native origin into:
1) words of Indo-European origin
2) words of Germanic origin
3) English proper words
woman, sister, glove, lady, tooth, slow, green, know, sand, long, grass, boy, seven, eat, widow, lip, swine, bird, corn, silver, ten, day, ship, we, sun, girl
-
Предмет:
Английский язык -
Автор:
caesar86 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
