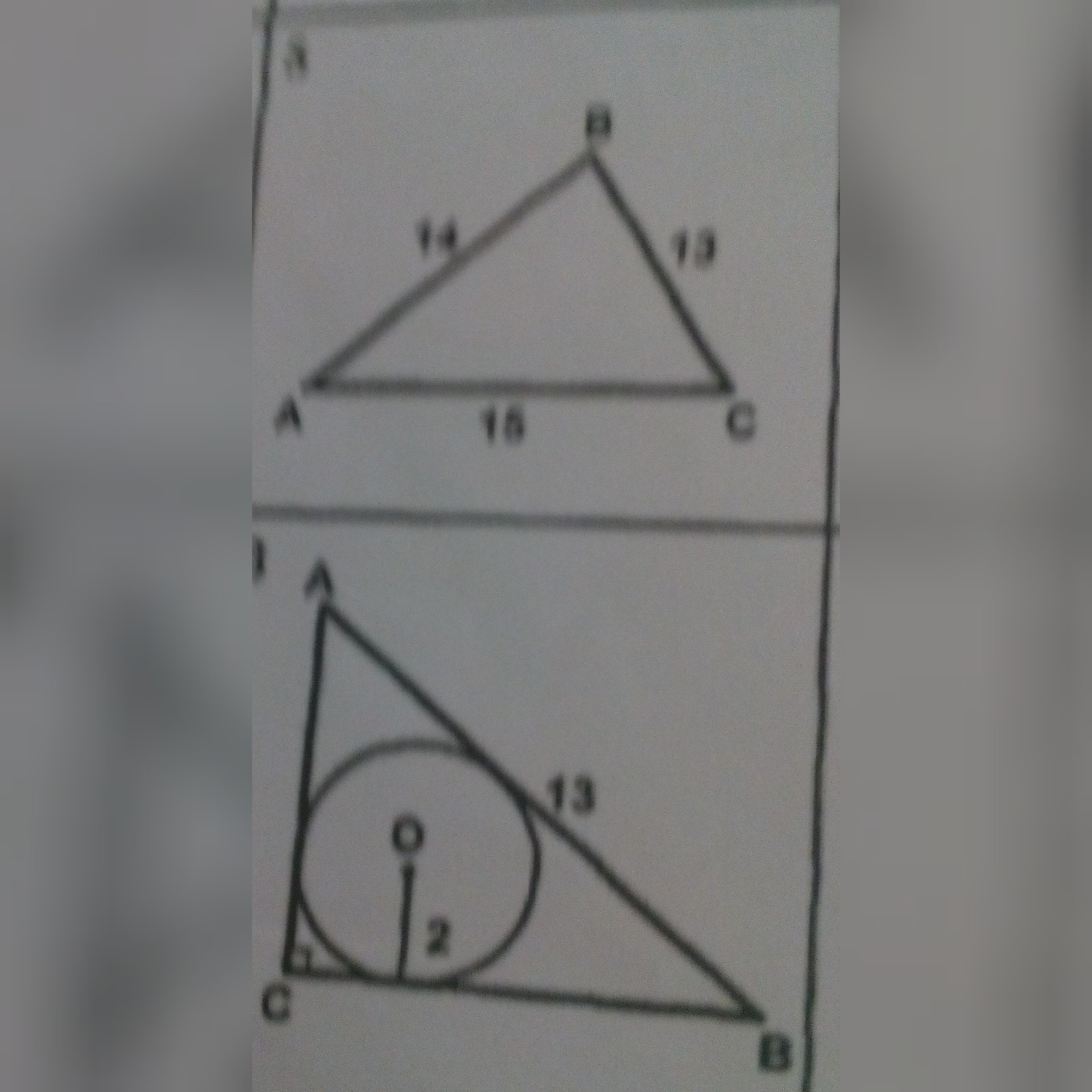
15 баллов найдите площадь треугольников 2 задачи пожалуйста срочно кто нибудь

Дано:∆ ABC, ∠C=90º,окружность (O, r) — вписанная,K, M, F — точки касания со сторонами AC, AB, BC,AB=13 , r=2 .Решение:1) Проведем отрезки OK и OF. OK перпендикулярен AC , OF перпендикулярен BC (как радиусы, проведенные в точки касания).Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).

2) По свойству касательных, проведенных из одной точки,AM=AK=x см,BF=BM=(13-x) см,CF=CK=r=2 . 3) AC=AK+KC=(x+2) , BC=BF+CF=13-x+2=(15-x) . По теореме Пифагора,АС^2+BC^2= AB^2(x+2)^2+(15-x)^2=13^2x^2+4x+4+225-30x+x^2=1692x^2-26x+229-169=02x^2-26x+60= 0   l:2x^2-13x+30=0D=169-120=49=7^2x1=(13-7): 2 =3x2=(13+7):2=10Если АМ=3 ,то АС=3+2=5(см) ,а BC=15-3=12 Если АМ=10 ,то АС=12(см),а BC= 15-10=54) S=1/2 AC*BC= 1/2*12*5= 30  Ответ 30 Задача 1 Формула герона S = √(p·(p - a)·(p - b)·(p - c)) ; √ - корень p= (a+b+c)/2 = (14 + 13 +15)/2= 21S=√(21*(21-14)*(21-13)*(21-15))=√(21*(7*8*6))=√(21*336)=√(7056)=84 Ответ 84