-
Исследовать функцию на экстремумы с помощью производной.
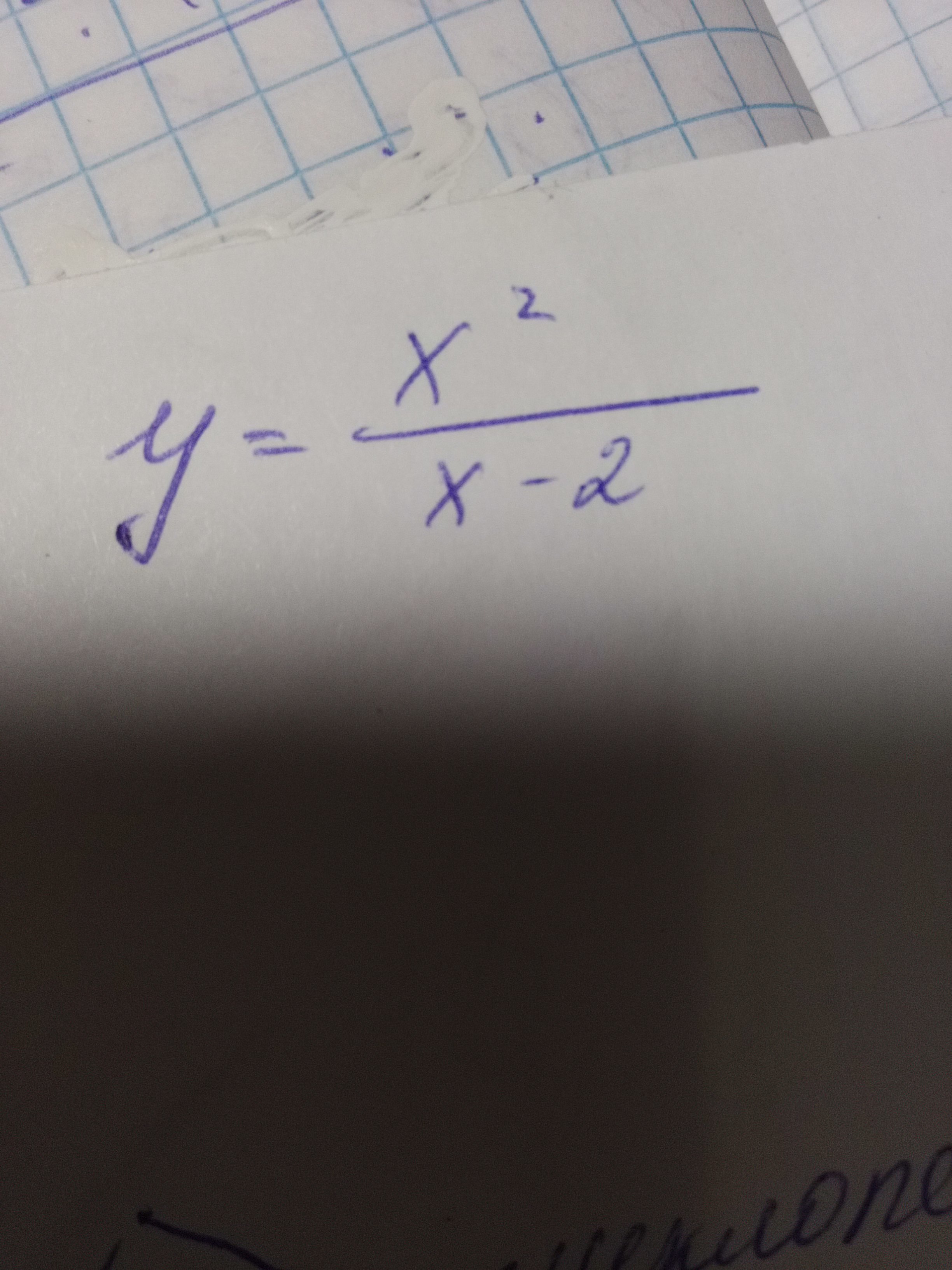
Ответы 2
-
Производная (2х(х-2)-х^2)/(х-2)^2=(х^2-4х)/(х-2)^2=(х(х-4))/(х-2)^2(х(х-4))/(х-2)^2=0х=0 и х=4; х≠2Хмах=4; Умах=8Хмин=0; Умах=0
-
Автор:
moniquelnyj - 5 лет назад
-
0
-
-
Исследовать функцию y = x² / (x -2) на экстремумы с помощью производной---------------------------------------------------1.ООФ (Область Определения Функции ) : x ∈(-∞; 2) ∪(2 ; ∞) * * * x ≠2 * * *2. x =2 является точкой разрыва второго родаLim x² / (x -2) = -∞ ; Lim x² / (x -2) = ∞ .x→2 - 0.......................x→2 + 03.График функции проходит через начало координат ( x =0 ; y =0).4. Экстре́мум _ максимальное или минимальное значение функции на заданном множестве . Если в точке x₀ есть экстремум, то либо значения y ' =0 либо не существует (вместе критические точки) и меняет знак при переходе через x₀._если при переходе через точку производная меняет знак с «плюса» на «минус», то в данной точке функция достигает максимума ;– если при переходе через точку производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума.-------Вычисляем производную данной функции (по формуле производной дроби)y ' = ( x² / (x -2) ) ' = ( (x²) ' *(x -2) - x²*(x -2)' ) / (x -2)² =(2x(x-2) -x²*1 ) /(x-2)²= =x(x - 4)/(x - 2)² .y ' = x(x - 4)/(x - 2)² . Найдем критические точки функции : y ' =0 или y ' не существует.а) y ' =0 x(x -4)/(x - 2)² =0 ⇒ x =0 или x = 4.b) Производная не существует в точке x =2 , но эта точка не принадлежит ООФ .--- Определяем промежутки монотонности функции (зависит от знака производной функции) Если :y ' < 0 ⇒ функция убывает (условно обозначаем знаком " ↓" ;y ' >0 ⇒ функция возрастает (условно обозначаем знаком " ↑" .методом интервалов:y ' "+" " -" "+" --------------------------------( 0) ---------- 2°------------ ( 4 ) ----------------------------y (возрастает) ↑ max (убывает)↓ min (возрастает) ↑ x =0 и x =4 являются точками экстремумовx =0 точка максимума → максимальное значение (локальное) :max (y) =y(0) = 0²/(0-2) = 0 ;x =4 точка минимума → минимальное значение(локальное):min(y) =y(4) = 4²/(4-2) =16/2 =8.ответ : Экстремумы : y=0 _ максимальное значение (локальное) в точке x =0 ; y=8 _ минимальное значение (локальное) в точке x =4.короче экстремумы y(0) = 0 →максимальное значение ; y(4) = 8 →минимальное значение.( Дополнительно и приведен график функции в прикрепленном файле)Удачи Вам !

-
Автор:
alicia97 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Реклама про мозаику из сыпучих материалов
-
Предмет:
Другие предметы -
Автор:
rosyuhur - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Назовите характерные запахи хлора и аммиака.
-
Предмет:
ОБЖ -
Автор:
ivoryflynn - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
"Не открывайте смс который
был отправлен от меня ,
не переходите по ссылке и
не устанавливайте .
Это вирус !!!
Предупреждаю!!! "
Правильно написала проверьте пожалуйста.
-
Предмет:
Русский язык -
Автор:
taco - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
областью определения функции 1/x-2 +3
a)x-любое
б)x-любое кроме 3
в)x-любое кроме 2 и 3
г)x-любое кроме 2
How much to ban the user?
1 hour
1 day
100 years
