Задать вопрос Регистрация
Помочь другим

  • Пробовал делить на cos^2a - некрасивые корни, которые не знаю как использовать, вряд-ли нужно было так решать, выразить ничего не выходит.

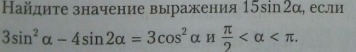
    question img

Ответы 4

  • ух, не заметил совсем что можно собрать косинус 2a, спасибо!)

    • Автор:

      caitlin
    • 5 лет назад
    • 0
  • А ведь тройки на это прям и наводить должны были... :)

    • Автор:

      acacio
    • 5 лет назад
    • 0
  • 3sin^2(a) - 4sin(2a) = 3cos^2(a)-4sin(2a) = 3(cos^2(a) - sin^2(a))sin(2a) = -3/4 cos(2a)tg(2a) = -3/43^2 + 4^2 = 9 + 16 = 25 = 5^2-> |sin(2a)| = 3/5П/2 < a < П -> П < 2a < 2П -> sin(2a) < 0sin(2a) = -3/515sin(2a) = -9
  • 3\sin^2 \alpha -4\sin2 \alpha =3\cos^2 \alpha \\ 3(\sin^2 \alpha -\cos^2 \alpha )-4\sin2 \alpha =0\\ -3\cos2 \alpha -4\sin2 \alpha =0\\ 3\cos2 \alpha +4\sin2 \alpha =0п/2 < a < п - вторая четверть. Синус положителен.tg2 \alpha =-\frac{3}{4} \\ 4\sin2 \alpha =-3\cos2 \alpha \\ 8\sin \alpha \cos \alpha =-3\cos^2 \alpha +3\sin^2 \alpha \\ 8tg \alpha =-3+3tg^2 \alpha \\ tg \alpha =t\\ 3t^2-8t-3=0\\ D=b^2-4ac=64+36=100\\ \\ t_1= \frac{8+10}{6} =3\\ \\ t_2= \frac{8-10}{6} =- \frac{1}{3} Корень t = 3 не подходит, т.к. во второй четверти тангенс отрицателен.Обратная заменаtg \alpha =- \frac{1}{3} Рассмотрим с помощью прямоугольного треугольника:Тангенс - отношение противолежащего катета к прилежащему катету1 - противолежащий катет3 - прилежащий катетпо т. Пифагора : √10 - гипотенузаСинус - отношение противолежащего катета к гипотенузе\sin \alpha = \frac{1}{ \sqrt{10} } Косинус - отношение прилежащего катета к гипотенузе:\cos \alpha =- \frac{3}{\sqrt{10}} Тогда окончательно имеем:15\sin2 \alpha =30\cdot\sin \alpha \cos \alpha =30\cdot \frac{1}{\sqrt{10}} \cdot(- \frac{3}{\sqrt{10}} )=-9Ответ: -9.

    • Автор:

      claudia91
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years