-
Помогите решить два примера Срочно надо
32*2^√x-1=4^√x-1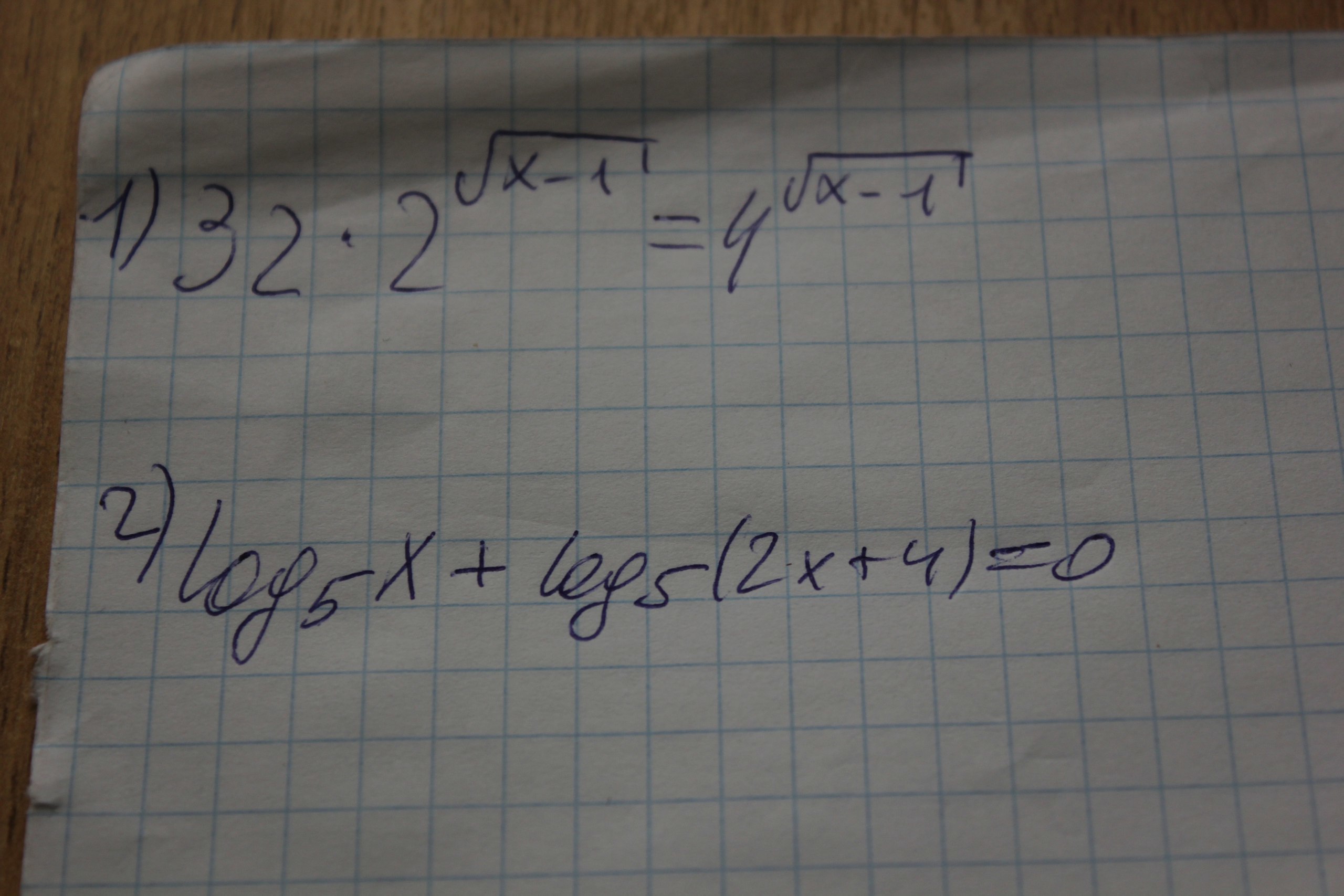
Ответы 2
-
1) Разделив обе части уравнения на 2^(√(x-1)), получим уравнение 32=2^(√(x-1)), или 2⁵=2^(√(x-1)). Отсюда √(x-1)=5, x-1=5²=25, x=25+1=26. Ответ: х=26.2) Применяя формулу суммы логарифмов, получаем log_5(x*(2*x+4))=0, x*(2*x+4)=5⁰=1, 2*x² +4*x-1=0, дискриминант D=16+8=24=(2*√6)², x1=(-4+2*√6)/4=√6/2-1, x2=(-4-2*√6)/4=-1-2√6. Но так как по свойству логарифма x>0, то x=√6/2-1. Ответ: x=√6/2-1.
-
Автор:
mauricio721 - 6 лет назад
-
0
-
-
Решение смотри на фото

-
Автор:
holden265 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Характерные признаки хордовый животных
-
мини соченение не меньше 10 предложений.
опишите внешность и характер Вашего
друга;
−
могут ли люди быть счастливы без
друзей;
−
важно ли быть другом для других.-
Предмет:
Другие предметы -
Автор:
gageular - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Планеты Солнечной системы.Законы Кеплера
-
Сочные листья встречаются у
Саксаула
Кукурузы
Картофеля
Огурца
Лука
How much to ban the user?
1 hour
1 day
100 years
