Срочно пожалуйста решите 533 и 534.Даю 20 баллов.Срочно надо!!!

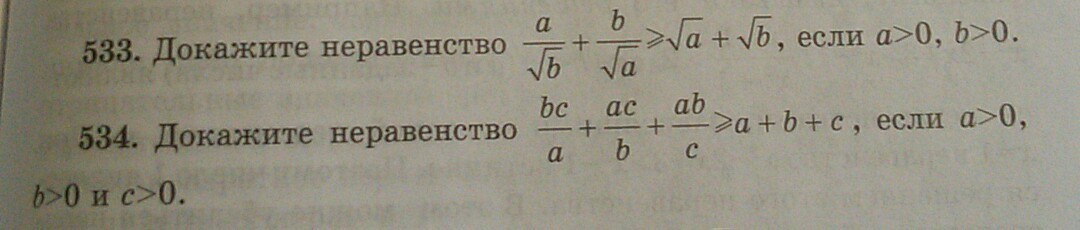
Ответы 1

533) $\frac{a}{ \sqrt{b} } + \frac{b}{ \sqrt{a} } \geq \sqrt{a} + \sqrt{b}$ $\frac{a}{ \sqrt{b} } + \frac{b}{ \sqrt{a} } = \frac{a \sqrt{a}+b \sqrt{b} }{ \sqrt{a}* \sqrt{b}} = \frac{( \sqrt{a} )^3+( \sqrt{b} )^3}{ \sqrt{a}* \sqrt{b}} = \frac{( \sqrt{a}+ \sqrt{b})(a- \sqrt{ab} +b)}{ \sqrt{ab} } =$ $=( \sqrt{a}+ \sqrt{b} )* \frac{a- \sqrt{ab}+b}{ \sqrt{ab}} \geq \sqrt{a}+ \sqrt{b}$ Нам надо это доказать. Докажем, что $\frac{a- \sqrt{ab}+b}{ \sqrt{ab}}\ \geq 1$ Умножим все на √(ab)a - √(ab) + b >= √(ab)a + b >= 2√(ab)(a + b)/2 >= √(ab)Это очевидно, среднее арифметическое двух чисел всегда больше или равно среднего геометрического.Равно - если числа равны, то есть при a = b.534) $\frac{bc}{a} + \frac{ac}{b} + \frac{ab}{c} \geq a+b+c$ $\frac{bc}{a} + \frac{ac}{b} + \frac{ab}{c}= \frac{b^2c^2+a^2c^2+a^2b^2}{abc}$ Дальше не знаю
- Автор:
  gabriellaharmon
- 4 года назад
- 0
Добавить свой ответ