-
Срочно пожалуйста решите 535,536.Даю 20 баллов. Пожалуйста помогите срочно! ! !
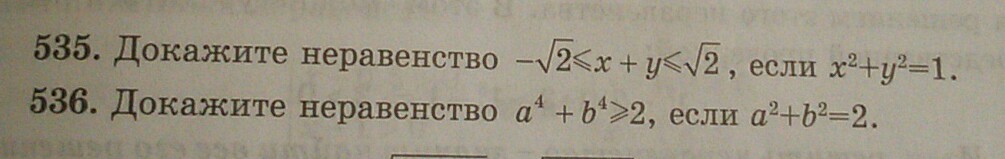
Ответы 1
-
536a²+b²=2 a²=2-b²a⁴+b⁴=(a²)²+2a²b²+(b²)²-2a²b²=(a²+b²)²-2a²b²(a²+b²)²-2a²b²≥24-2a²b²≥22a²b²≤2a²b²≤1(2-b²)*b²≤12b²-b⁴-1≤0(b²-1)²≥0Квадрат всегда больше равен 0 чтд535-√2≤x+y≤√2x²+y²=1вспомним основное тригонометрическое равенствоsin² x + cos² x = 1пусть x=sinx y=cosx (имеем право если есть такое равенство)тогда -√2≤sinx+cosx≤√2находя минимум и максимум sinx+cosx получаем что минимум при sinx=cosx=-√2/2 максимум при sinx=cosx=√2/2минимум -√2/2-√2/2=√2максимум √2/2+√2/2=√2значит -√2≤sinx+cosx≤√2 jобратная замена -√2≤x+y≤√2 чтд
-
Автор:
jimena - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
m=320кг
s=0,08m²
p=20кПа
P=? -
х квадрат - 4х + 3 если х=2+ корень 3
-
Предмет:
Алгебра -
Автор:
jazlynna5r8 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
З точки К до кола з центром О проведено дотичні КС і КМ, К і М — точки дотику, ∡ОСМ = 40°. Знайди кут СКМ.
-
Предмет:
Геометрия -
Автор:
isaiahramirez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Срочно пожалуйста решите 537 и 538.Даю 20 баллов. Пожалуйста помогите срочно! ! !
How much to ban the user?
1 hour
1 day
100 years
