Задать вопрос Регистрация
Помочь другим

  • 100 баллов + лучший ответ! Найти корни иррационального уравнения:

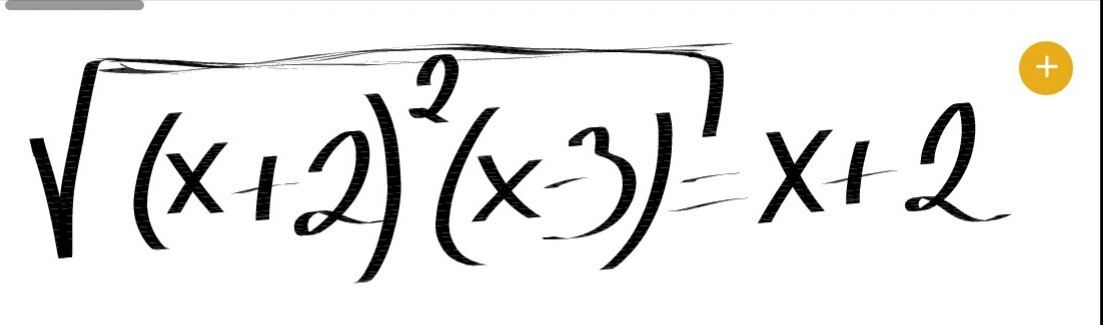
    question img

Ответы 7

  • Согласен, получилось не очень рационально, т.к решилось "в лоб"

    • Автор:

      andreiyrv
    • 5 лет назад
    • 0
  • Предлагаю вам дать свой ответ, более простой

    • Автор:

      faith
    • 5 лет назад
    • 0
  • Хотите пошлю на исправление?
  • Кстати, возведение в квадрат не есть равносильный переход. Поэтому что-то вроде проверки нужно сделать

    • Автор:

      alliekjrk
    • 5 лет назад
    • 0
  • Хорошо, хотя это и очевидно, давайте исправлю
  • \\ (x-3)(x+2)^2=(x+2)^2 \\ (x-3)(x+2)^2-(x+2)^2=0 \\ (x+2)^2(x-3-1)=0 \\ 1) (x+2)^2=0 \\ x+2=0 \\ x=-2 \\2)x-4=0 \\x=4Выполним проверку на посторонние корни :   \sqrt{(-2+2)^2(-2-3)} =-2+2 \\ 0=0 \\ \sqrt{(4+2)^2(4-3)} =4+2 \\ 6=6  Ответ: x=4 или x=-2

    • Автор:

      petty34
    • 5 лет назад
    • 0
  • возводим обе части в квадрат, но:(x+2)^2*(x-3)>=0 и x+2>=0(x+2)^2*(x-3)=(x+2)^2переносим все в одну часть и выносим (x+2)^2 за скобки:(x+2)^2*(x-3-1)=0по свойству произведения:(x+2)^2=0x+2=0x=-2илиx-3-1=0x-4=0x=4проверяем:6^2*(4-3)>=0 - верно6>=0 -верно0*(-5)>=0 - верно0>=0 - верноОтвет: x1=-2; x2=4

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years