-
100 баллов + лучший ответ! При каком наибольшем целом значении параметра а система уравнений имеет два решения? (с подробным решением)
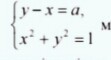
-
Предмет:
Алгебра -
Автор:
rosaosborne - 5 лет назад
-
Ответы 2
-
Из первого уравнения выразим у, т.е.
и подставим во второе уравнение
D>0 - уравнение имеет 2 корня, т.е.
или
откуда
Наибольшее значение а=1.
-
Автор:
rexnkps - 5 лет назад
-
0
-
-
то же самое но на пальцах второе уравнение - окружность с центром в начале координат, радиусом 1первое уравнение - прямая под углом 45 градусов, смещенная относительно начала координат вверх на "а"очевидно что такая прямая может иметь общие точки с окружностью в диапазоне от минус до плюс корень из двух. причем в названных точках только одно решение. наибольшее целое значение параметра а при котором именно две точки пересечения это а=1

-
Автор:
scrappydpfa - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решить пример 18:39+76 сколько получится
-
Предмет:
Математика -
Автор:
adelaidamartinez - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
корень 72 - корень 8
1)8 2)16 корень 2 3)4 корень 2 4)9
с решением-
Предмет:
Математика -
Автор:
kendrickbriggs - 5 лет назад
-
Ответов:
2 -
Смотреть
-
- Найдите AD, если в прямоугольном треугольнике ABC ( ∠C = 90°) CD ⊥АВ , АС = m и ВС = n
-
решите уравнение |х+4|=12
помогите плиз!!!-
Предмет:
Математика -
Автор:
grant87f8 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
