-
14. Освободите выражение от иррациональности в знаменателе.
а) √(y+1)
б)2√(y+1)
в)√(y+1)/y+1
г)√(y+1)/y+2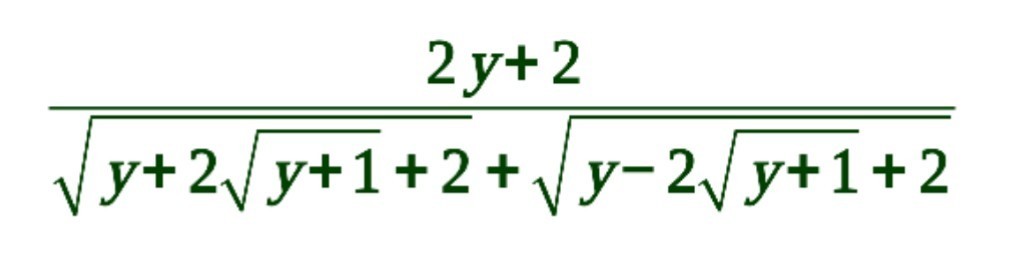
Ответы 1
-
-
Автор:
jacob89 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решите пример пж (14+50)*13-(80*12-194)
-
Предмет:
Математика -
Автор:
andrew - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите уравнение
0,3*(5х+0,2)=-2,6-(2,7х-1,4)-
Предмет:
Математика -
Автор:
crystal4 - 5 лет назад
-
Ответов:
6 -
Смотреть
-
-
Тема и идея рассказа Толстый и тонкий
-
Предмет:
Литература -
Автор:
jamar - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Нужно решить систему уравнения
3/Х-4/у=1.
2/Х+5/у=4,5-
Предмет:
Математика -
Автор:
ariellabray - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
