Ребята помогите с 8 12 19 номерами!!!! ПОЖАЛУЙСТА Тема биквадратные уравнения

Ребята помогите с 8 12 19 номерами!!!! ПОЖАЛУЙСТА Тема биквадратные уравнения
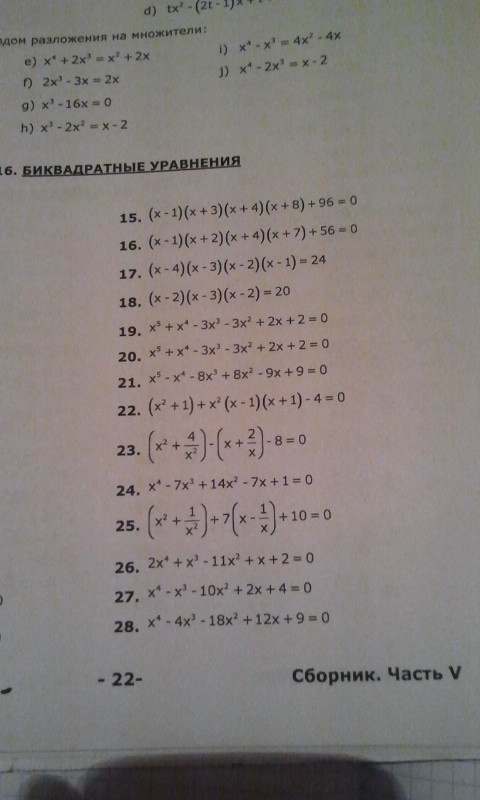
- Предмет:
  Алгебра
- Автор:
  puffyclements
- 5 лет назад

Ответы 5

drwndможешь еще решить
- Автор:
  bongowp3l
- 5 лет назад
- 0
что?
- Автор:
  miasy
- 5 лет назад
- 0
я щас добавлю
- Автор:
  pigletkyqu
- 5 лет назад
- 0
18 И 24
- Автор:
  toby7
- 5 лет назад
- 0
ну что мы здесь делаем, приводим к стандартному виду 8. $(x^2-x)^2-8x^2+8x+12 = 0$ $(x^2-x)^2-8(x^2-x)+12 = 0$ замена: $x^2-x = a$ $a^2-8a+12=0$ по теореме Виета: $\left \{ {{a_{1}+a_{2} = -b} \atop {a_{1}*a_{2}=c}} ight.$ $a_{1} = 6$ $a_{2} = 2$ обратная замена: $x^2-x = 6$ $x^2-x-6=0$ $D = 25 = 5^2$ $x_{1} = \frac{1+5}{2} =3$ $x_{2}= \frac{1-5}{2} =-2$ $x^2-x = 2$ $x^2-x-2=0$ $D = 9 =3^2$ $x_{3} = \frac{1+3}{2} =2$ $x_{4} = \frac{1-3}{2} =-1$ 12. вот лично я в таких случаях люблю использовать метод Горнера (ладно, я вообще очень люблю применять его, когда речь заходит об уравнениях высших степеней)раскрыв скобки, имеем $x^4-6x^3+11x^2-6x-24=0$ $(x-4)(x^3-2x^2+3x+6)=0$ $(x-4)(x+1)(x^2-3x+6)=0$ $x_{1}=4$ $x_{2}=-1$ $x^2-3x+6=0$ $D = 9-24$ - корней нет19. снова метод Горнера (с его сутью подробно можно ознакомиться на многих веб-ресурсах) $x^5+x^4-3x^3-3x^2+2x+2 = 0$ $(x-1)(9x^4+2x^3-x^2-4x-2)=0$ $x_{1}=1$ $(x-1)(x+1)(x^3+x^2-2x-2)=0$ $(x-1)(x+1)^2(x^2-2)=0$ $x_{2,3}=-1$ $x^2-2=0$ $x^2=2$ $x_{4}=б \sqrt{2}$
- Автор:
  steven599
- 5 лет назад
- 0
Добавить свой ответ