-
Решите неравенство.
Пожалуйста, напишите подробное решение.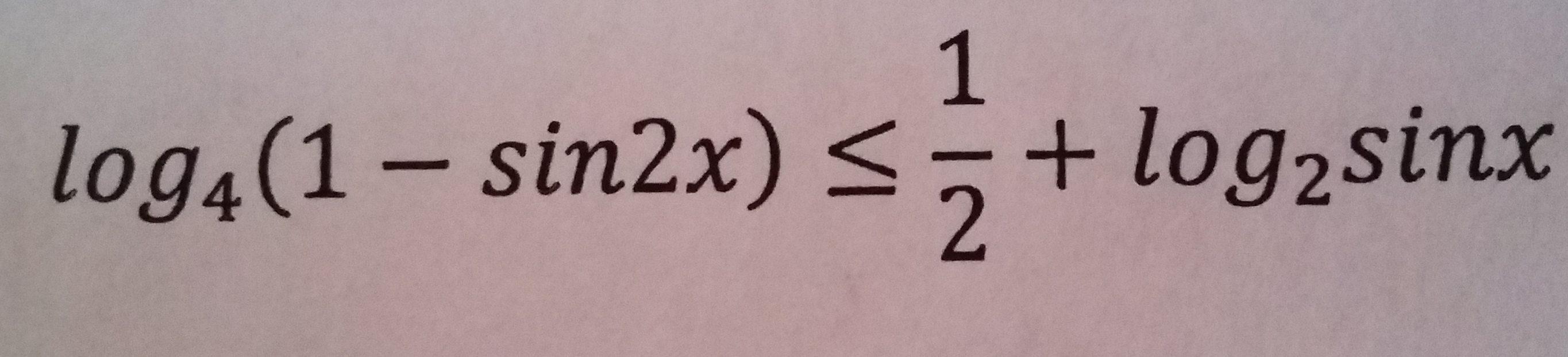
-
Предмет:
Алгебра -
Автор:
zayneraymond - 6 лет назад
-
Ответы 2
-
Ответ: x E [arcctg(1 + sqrt(2)) + 2pn; arcctg(1 - sqrt(2)) + 2pn]
-
Автор:
fellowf1kl - 6 лет назад
-
0
-
-
Сначала решаем как логарифмическое уравнение, для этого приведем к одинаковому основанию и внесем под знак логарифма дробь 1/2.log2(x) = 2log4(x), это должно быть понятно.log4(1 - sin(2x)) <= 1/2 + 2log4(sin(x))log4(1 - sin(2x)) <= log4(2) + 2log4(sin(x))log4(1 - sin(2x)) <= log4(2) + log4(sin(x)) + log4(sin(x))log4(1 - sin(2x)) <= log4(2) + log4(sin^2(x))log4(1 - sin(2x)) <= log4(2*sin^2(x))Так как основание логарифма (4) больше 1, это неравенство эквивалентно следующему:1 - sin(2x) <= 2*sin^2(x)Решим его.Пусть s = sin(x), c = cos(x), C = ctg(x). Тогда получим:2ss - 1 + 2sc >= 0Рассмотрим 2 случая:1) sin(x) = 0. В этом случае cos(x) = 10 - 1 + 0 >= 0Неравенство решений не имеет.2) sin(x) <> 0. В этом случае имеем возможность разделить неравенство на sin^2(x) > 0. Получим:2 - 1/(ss) + 2c/s >= 02 - 1/(ss) + 2C >= 0В учебнике должна быть такая формула:1 + CC = 1/(ss)Применив ее и выразив 1/(ss) через котангенс получим:2 - 1 - CC + 2C >= 01 - CC + 2C >= 0CC - 2C - 1 <= 0, где C = ctg(x)А это уже квадратное уравнение. Решим его:D = 4 + 4*1 = 8C1,2 = (2 +- sqrt(8))/2sqrt(8) это корень квадратный из 8.Промежуточный ответ:x = arcctg((2 + sqrt(8))/2) + pn = arcctg(1 + sqrt(2)) + pn x = arcctg((2 - sqrt(8))/2) + pn = arcctg(1 - sqrt(2)) + pnТут еще нужно не забыть про ОДЗ, т. к. аргумент логарифмической функции должен быть больше нуля.sin(x) > 0 выполняется при x E (0 + 2p; p + 2p)1 - sin(2x) > 0 выполняется всегда кроме x = p/4Поэтому ответ такой:x = arcctg(1 + sqrt(2)) + 2pnx = arcctg(1 - sqrt(2)) + 2pn
-
Автор:
lyla - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
3^2*9^3/3^5
3^2x9^3
------------
3^5
Упростите выражение
-
Предмет:
Математика -
Автор:
rexybenjamin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Документ HTML должен
заканчиваться тегом:
А)-
Предмет:
Информатика -
Автор:
abigail - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Токар повинен виготовити за певний час 70 деталей. Щодня вiн виготовляв на 2 деталi бiльше, нiж планував, i виконав завдання на 4 днi ранiше строку. Скiльки деталей за день виготовляв токар?
-
Помогите сделать краткое содержагие былины "Добрыня Никитич " ! 5-6 предложений .
-
Предмет:
Литература -
Автор:
claudialikq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
