Задать вопрос Регистрация
Помочь другим

  • Помогите доказать:
    (a+b) × (1/a + 1/b) > = 4, если a>0, b>0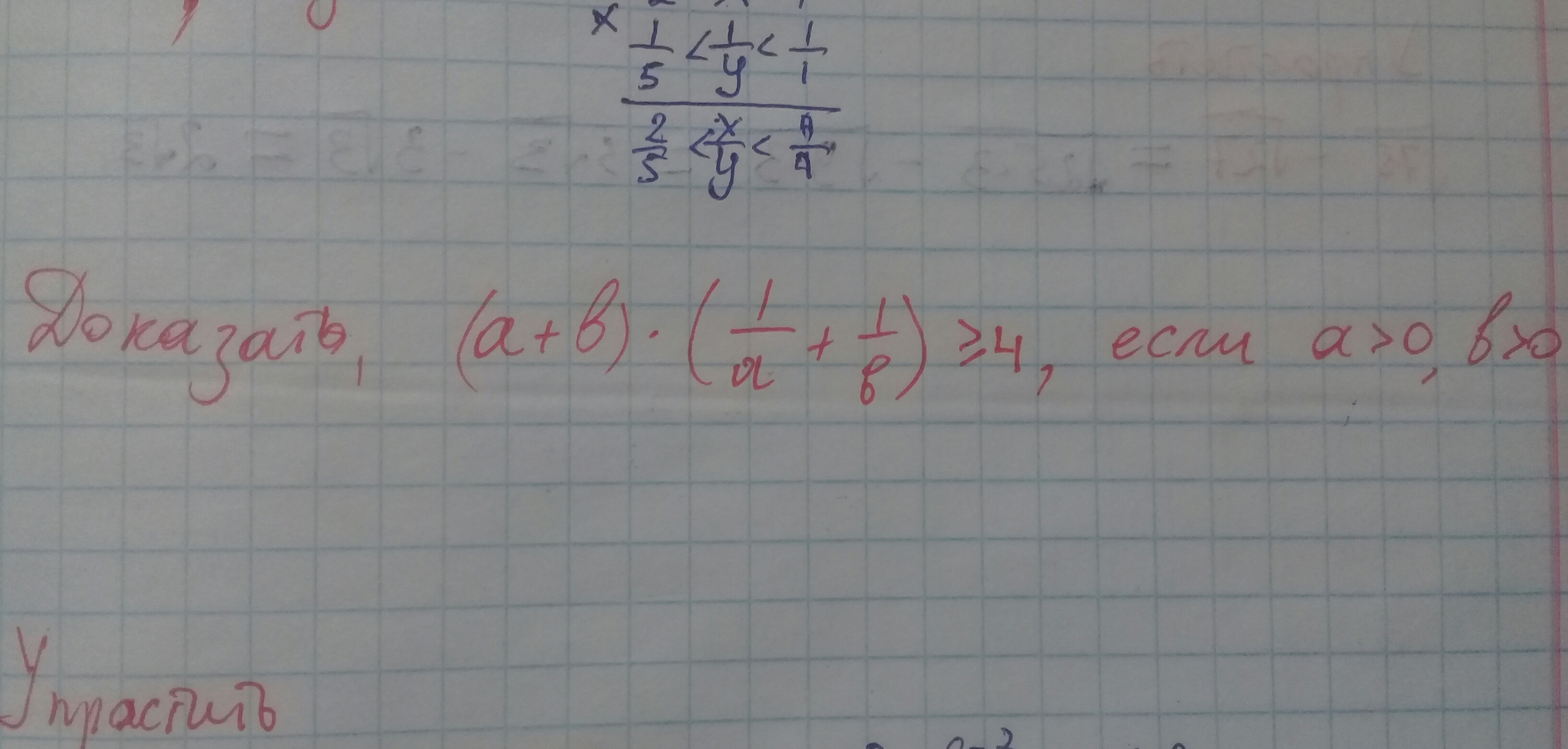

    question img

Ответы 1

  • (a+b)( \frac{1}{a} + \frac{1}{b} ) \geq 4 \\ a\ \textgreater \ 0 \ \ \ \ \ b\ \textgreater \ 0\\ \frac{a}{a} + \frac{a}{b} + \frac{b}{a} + \frac{b}{b} \geq 4\\ 2+ \frac{a}{b} + \frac{b}{a} \geq 4\\ \frac{a}{b} + \frac{b}{a} \geq 2\\ \frac{a^2+b^2-2ab}{ab} \geq 0\\ \frac{(a-b)^2}{ab} \geq 0\\(a-b)^2 \geq 0\ \ \ \ \ ab\ \textgreater \ 0     Числитель всегда неотрицателен т.к в квадрате, знаменатель больше нуля, т.к a>0 и b>0

    • Автор:

      catwoman
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years