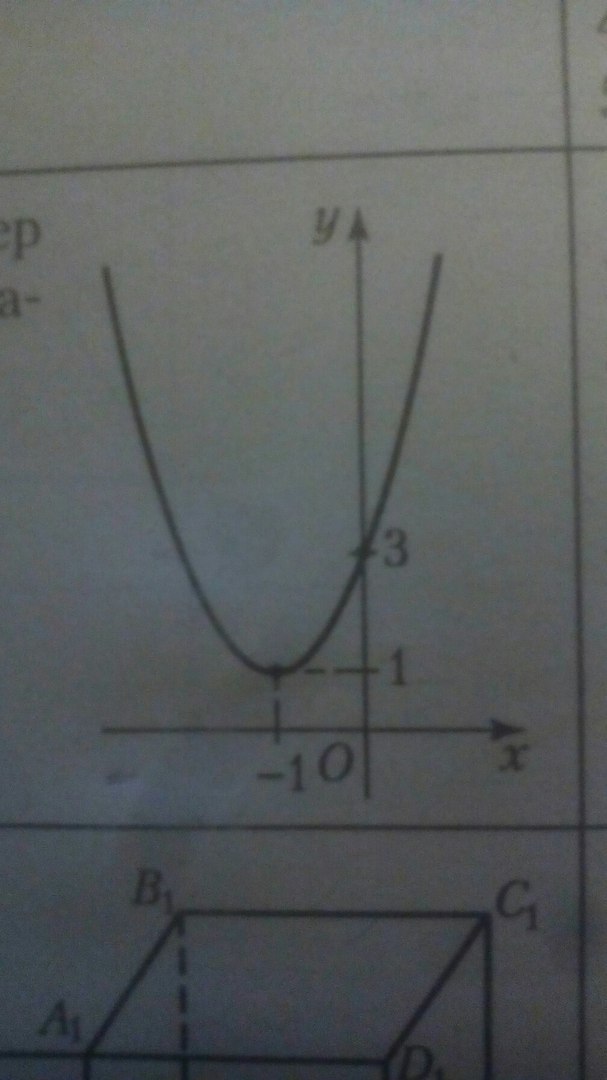
На рисунке изображен график квадратичной функции, уравнение которой имеет вид:

Вершина параболы имеет координату (-1; 1). Прямая x = -1 - ось параболы.Парабола пересекает ось Oy в точке А(0; 3). Тогда точка, симметричная точке А относительно прямой x = -1, будет иметь координаты (-2; 3).Итак, парабола проходит через точки A(0; 3), B(-2; 3), C(-1; 1).Уравнение параболы имеет вид y = ax² + bx + c.Найдём коэффициенты a, b и c, подставив в уравнение параболы координаты точек:3 = 0·a + 0·b + c3 = 4a - 2b + c1 = a - b + cc = 33 = 3 + 4a - 2b1 = a - b + 3c = 34a = 2b-2 = a - bc = 3b = 2a-2 = a - 2ac = 3a = 2b = 4Значит, парабола имеет вид y = 2x² + 4x + 3.Ответ: y = 2x² + 4x + 3. Второй способ:График функции y = a(x - m)² + l получаем из графика функции y = x² сужением к оси Oy с коэффициентов a, переносом на m ед. вправо, если m > 0, на m ед. влево, если m < 0,переносом на l ед. вверх, если l > 0, вниз, если l < 0.По графику сразу видно, что вершину перенесли на 1 ед. влево и на 1 ед. вверх, к тому же, график сжали к оси Oy с коэффициентом 2.Значит, y = 2(x + 1)² + 1 y = 2x² + 4x + 2 + 1y = 2x² + 4x + 3Ответ: y = 2x² + 4x + 3.