-
Решите пожалуйста.
Надо найти а, когда единственное решение.
Пример в файле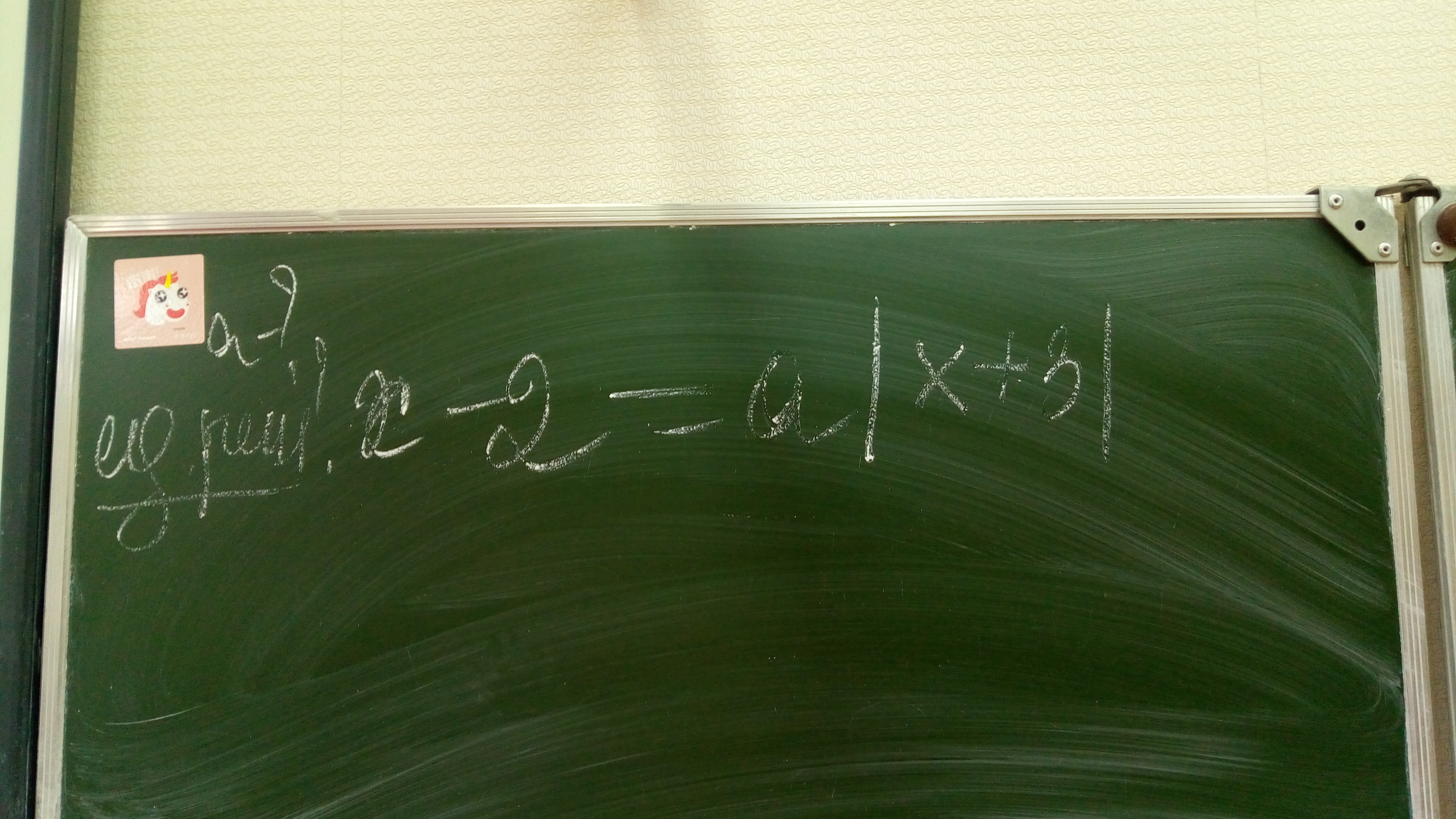
Ответы 1
-
task/25128873--------------------уравнение x-2 = a|x+3| имеет единственное решение , a -? .----------------* * * x = -3 ⇒ x -2 =0 ⇔ x =2 , т.е. не может x =3 * * *1) x < - 3 * * *x-2 =- a(x+3) ⇔(a+1)x = 2 -3a имеет единственное решение, если a≠ -1x = (2 -3a) / (a+1) ; причем должно выполнятся (2 -3a) / (a+1) < - 3 (2 -3a) / (a+1) +3 < 0 ⇔ 5/(a+1) < 0 ⇒ a < -1. 2) x > - 3x-2 = a(x+3) ⇔(1 - a)x = 2 +3a имеет единственное решение, если a≠ 1x =( 2 +3a ) / (1-a) ; причем должно выполнятся (2 +3a) / (1-a) > -3 (2+3a) / (1-a) +3 > 0 ⇔5 / (1-a) >0 ⇒ a < 1. 1) /////////////////////// ---------------------- ( -1) --------------- (1)2) //////////////////////////////////////////ответ : a ∈ [-1 ; 1) .
-
Автор:
buttonspierce - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
катер шел 2 ч по течению реки и 3 ч против течения.какой путь проделал катер за эти 5 ч,если собственная скорость теплохода 11,3км/ч ,а скорость течения реки 2,2 км/ч.
-
Предмет:
Математика -
Автор:
chica - 6 лет назад
-
Ответов:
7 -
Смотреть
-
- Профессионал связанные с биологией
-
сколько в 1 агре кв метров
-
Предмет:
Математика -
Автор:
alonzomnek - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Помогите!решите пример 505/54-(65+65)-650:76×6=?
-
Предмет:
Математика -
Автор:
roderickhooper - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
