-
Алгебра 11 класс - производная. Решите, пожалуйста, в) и г) :)
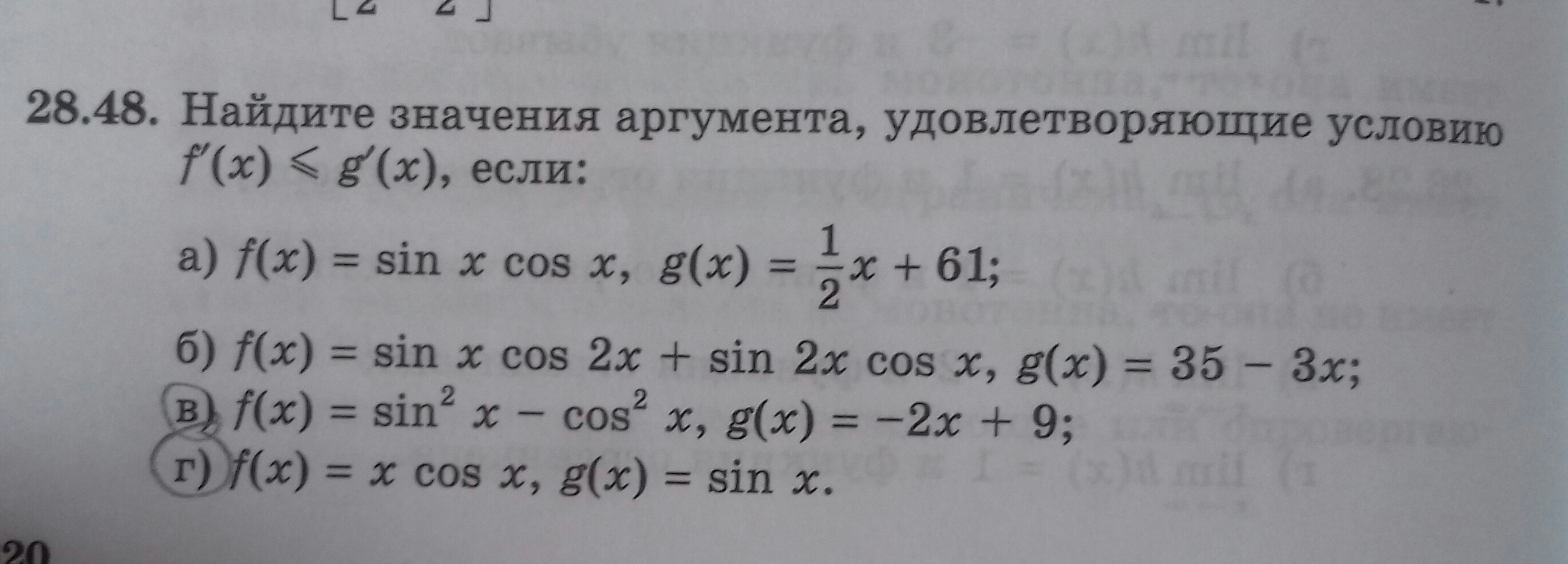
-
Предмет:
Алгебра -
Автор:
nathanielbrooks - 5 лет назад
-
Ответы 1
-
в) f(x) = sin²x - cos²x = -(cos²x - sin²x) = -cos2xf'(x) = (-cos2x)' = 2sin2xg(x) = -2x + 9g'(x) = (-2x + 9)' = -22sin2x ≤ -2sin2x ≤ -1Неравенство выполняется только тогда, когда sin2x = -1.sin2x = -12x = -π/2 + 2πn, n ∈ Zx = -π/4 + πn, n ∈ ZОтвет: x ∈ {-π/4 + πn}, n ∈ Z.г) f(x) = xcosxf'(x) = (x)'cosx + x·(cosx)' = cosx - xsinx g(x) = sinxg'(x) = (sinx)' = cosxcosx - xsinx ≤ cosx-xsinx ≤ 0xsinx ≥ 0h(x) = xsinxh(-x) = -x·sin(-x) = xsinxЗначит, график функции симметричен относительно начала отсчёта.Тогда достаточно рассмотреть промежуток [0; +∞)первый множитель (множитель x) можно убрать, т.к. он не влияет на решение неравенства:sinx ≥ 02πn ≤ x ≤ π + 2πn, n ∈ Z.В силу чётности функции получаем (симметрии относительно оси Oy), что -π + 2πn ≤ x ≤ π + 2πn, n ∈ Z.Ответ: -π + 2πn ≤ x ≤ π + 2πn, n ∈ Z.
-
Автор:
glennzxps - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Колыбельные песни пестушки потешки заклички приговорки считалки скороговорки. Приведите пример
-
Предмет:
Литература -
Автор:
crackersbrewer - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
туристы за два дня прошли 44км. в 1 день они были в пути 5часов а во 2 6часов.какое растояние прошли туристы в каждый из жтих дней если они шли с одинаковой скоростью
-
Предмет:
Математика -
Автор:
loverep6u - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Подскажите пожалуйста как решить уравнение (4,2+x)÷6=0,9
Зарание спасибо!
-
Предмет:
Математика -
Автор:
doggon’mwgj - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- считаете ли вы что реформы Сперанского могли бы принципиально изменить Россию направил ее по более благоприятному пути
How much to ban the user?
1 hour
1 day
100 years
