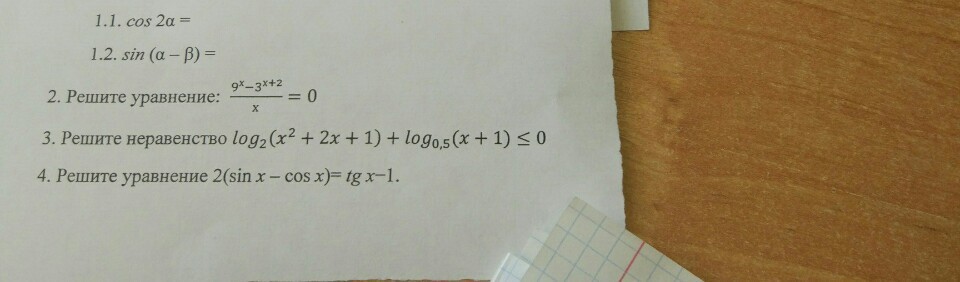Ответы 2
-
Решение смотри на фото

-
Автор:
holden265 - 5 лет назад
-
0
-
-
task/25353447-------------------- см. приложение3. решите неравенство Log(2) (x² +2x+1) + Log(0,5) (x+1) ≤ 0 .-------Log(2) (x² +2x+1) + Log(2⁻¹ ) (x+1) ≤ 0 ;2Log(2) (x+1) - Log(2) (x+1) ≤ 0 ; * * * ОДЗ: x+1 >0 * * *Log(2) (x+1) ≤ Log(2) 1 ;0< x+1 ≤1⇔ -1 < x ≤ 0 . ответ : x ∈ ( -1 ; 0 ] .-------4. Решите уравнение 2(sinx - cosx) = tgx -1.-------2(sinx - cosx) =sinx / cosx -1 ; * * * ОДЗ: cosx ≠ 0 ⇒x ≠π/2 +πn , n ∈ Z * * *2(sinx - cosx)cosx =(sinx - cosx) ;2(sinx - cosx)(cosx -1/2) =0 ;а)sinx -cosx = 0 ; * * * √2sin(x-π/4) =0⇒ x - π/4 = πn * * *sinx =cosx || : cosx ≠0 tgx =1 ;x= π/4 +πn ,n ∈ Z.б)cosx -1/2 = 0 ;cosx =1/2 ;x =± π/3 +2πk , k∈Z.ответ : π/4 +πn , n ∈ Z ± π/3 +2πk , k∈Z .

-
Автор:
buttercupvdd0 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решите уравнения:
(m-0,67)*0,02=0,0152
(y-15,7):19,2=4,7
прошуу. очень срочно-
Предмет:
Математика -
Автор:
braxtonuttf - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
ДАЮ 100 баллов
СХЕМА ПРЕДЛОЖЕНИЕ .
В школьном саду учащиеся обрезали сухие листья сучья на ФРУКТОВЫХ ДЕРЕВЬЕВ ЯБЛОНЬ И ГРУШ.
-
Предмет:
Русский язык -
Автор:
schultz46 - 5 лет назад
-
Ответов:
8 -
Смотреть
-
-
Формула спиртового розчину йоду
-
Предмет:
Химия -
Автор:
donnabraun - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Помогите пожалуйста
Замерзает ли море Лаптевых ?
И какова солёность моря Лаптевых ?
How much to ban the user?
1 hour
1 day
100 years