Решите пределы!!! По 1 и 2 способу замечательных пределов

Решите пределы!!! По 1 и 2 способу замечательных пределов
- Предмет:
  Алгебра
- Автор:
  apollo74
- 5 лет назад

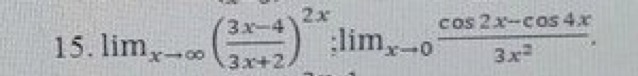
Ответы 2

Можно на листке всё написать?
- Автор:
  callum
- 5 лет назад
- 0
1. Выделяем целую часть, чтобы решить через 2 замечательный предел. $\lim_{x \to \infty} (\frac{3x-4}{3x+2})^{2x} = \lim_{x \to \infty} (\frac{3x+2 - 6}{3x+2})^{2x} = \lim_{x \to \infty} ( 1 +\frac{-6}{3x+2})^{2x}$ = $\lim_{x \to \infty} [(1+ \frac{-6}{3x+2})^{ \frac{3x+2}{-6} }]^{2x* \frac{-6}{3x+2} }$ = $\lim_{x \to \infty} e^{ 2x* \frac{-6}{3x+2} } } = e^{\lim_{x \to \infty} 2x* \frac{-6}{3x+2} } = e^{ \lim_{x \to \infty} \frac{-12x}{3x+2} } = \lim_{x \to \infty} \frac{-12}{3+ \frac{2}{x} }$ = $e^{-4} = \frac{1}{e^4}$ 2.Для начала давай упростим числитель с помозью формул приведения: $cos(2x) - cos(4x) = 1 - 2xin^2(x) - (1 - 2sin^2(2x)) =$ = $2sin^2(2x) - 2sin^2(x) = 2(sin^2(2x) - sin^2(x)) =$ = $2(4sin^2(x)cos^2(x) - sin^2(x))$ Этого достаточно, теперь запишем предел. $\lim_{x \to 0} \frac{2(4sin^2(x)cos^2(x) - sin^2(x))}{3x^2}$ Выносим 2/3 за предел: $\frac{2}{3} lim_{x \to 0}\frac{(4sin^2(x)cos^2(x) - sin^2(x))}{x^2}$ Теперь поделим всё на x². Так как предел произведения равен произведению пределов, то получим: $\frac{2}{3} ( lim_{x \to 0} \frac{4sin^2x}{x^2}* lim_{x \to 0} cos^2(x) - lim_{x \to 0} \frac{sin^2(x)}{x^2})$ cos(0) = 1 $\frac{2}{3} ( 4*lim_{x \to 0} (\frac{sin(x)}{x})^{2}* 1 - lim_{x \to 0} (\frac{sin(x)}{x})^2)$ = $\frac{2}{3} ( 4*(lim_{x \to 0} \frac{sin(x)}{x})^{2}* 1 - (lim_{x \to 0} \frac{sin(x)}{x})^2)$ = $\frac{2}{3}( 4 - 1) = 2$
- Автор:
  autumnphillips
- 5 лет назад
- 0
Добавить свой ответ