-
Пожалуйста помогите с решением задания 278 , с пояснением!!!!!
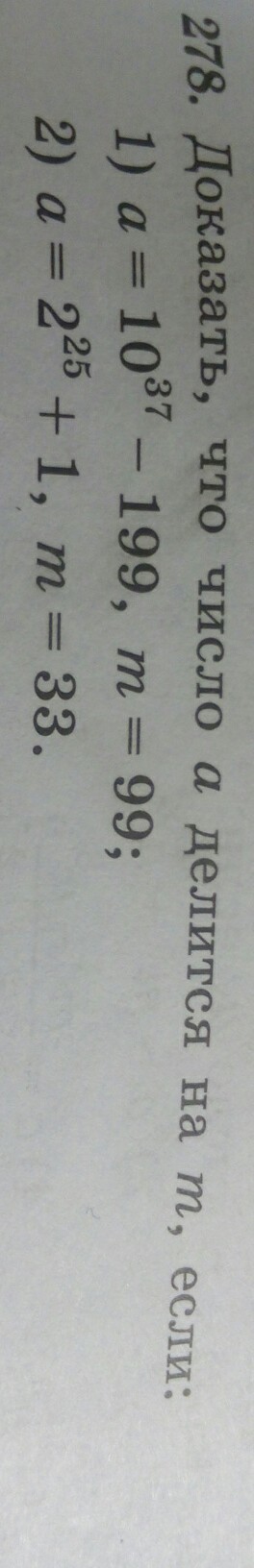
-
Предмет:
Алгебра -
Автор:
marilynha3b - 5 лет назад
-
Ответы 1
-
1)
делится на 99. Добавим к a 99, умноженное на 2 - делимость на 99 при этом не изменится, а число упростится:
(всего 36 девяток). Теперь можно или просто разделить получившееся число на 99 - получится
(18 единиц и 17 нулей), или сослаться на признаки делимости на 9 (сумма цифр должна делиться на 9) и на 11 (сумма цифр с чередованием знаков должна делиться на 11).2)
(математики говорят так: число 2 в пятой степени сравнимо с минус 1 по модулю 33. А тогда
(то есть два в десятой сравнимо с 1 по модулю 33; иными словами, два в десятой дает остаток 1 при делении на 33). Можно сказать, что
.А тогда
(соображайте сами, что это за B там возник). То есть два в двадцатой сравним с 1 по модулю 33. А два в пятой был сравним с минус единицей по модулю 33. Если Вы правильно поняли мои рассуждения, Вам несложно будет сообразить, что отсюда следует, что
будет сравним с минус единицей, а тогда
будет сравним с нулем по модулю 33. Что и означает, что это число делится на 33.
-
Автор:
haydenmbyo - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОЧНО ОЧЕНЬ!!!!!!!!!!!!
Найди значения выражений x²−2xy+y² и (x−y)² и сравни их, если
x=-9,5 и y=-2,1-
Предмет:
Алгебра -
Автор:
addysonsalazar - 5 лет назад
-
Ответов:
0 -
Смотреть
-
- Вставьте пропущенное слово в характеристике оксида натрия : белое твердое вещество , в растворяется с образованием ... , С кислотами образует ... И воду , проявляет ... Свойства
-
Як, по-вашому, дорослість і самостійність виявляються в навчанні?
-
Предмет:
Українська література -
Автор:
jaylynn - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Высота,проведенная к основанию равнобедренного треугольника, равна 8,2см а боковая сторона треугольника равна 16,4см .Найдите углы этого треугольника ... срочно Пожалуйста .
-
Предмет:
Геометрия -
Автор:
skylerfrey - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
