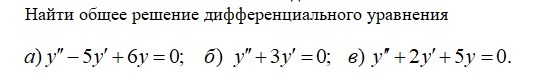Ответы 2
-
в последнем ответе наверное можно еще вынести общий множитель e^(-x) за скобку , а так конечно браво маэстро
-
Автор:
biancaarmstrong - 6 лет назад
-
0
-
-
Все три решаются через составление характеристического уравненияа) y''- 5y' + 6y = 0k^2 - 5k + 6 = 0(k - 2)(k - 3) = 0k = 2, k = 3y = C1 * e^2x + C2 * e^3xб) y'' + 3y' = 0k^2 + 3k = 0k(k + 3) = 0k = 0, k = -3y = C1 + C2 * e^(-3x)в) y'' + 2y' + 5y = 0k^2 + 2k + 5 = 0k^2 + 2k + 1 = -4(k + 1)^2 = -4k + 1 = +-2ik = -1 +- 2iy = C1 * e^(-x) * cos(2x) + C2 * e^(-x) * sin(2x)
-
Автор:
dustin23 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как правильно перевести время в этом тексте МЕНІҢ КҮН ТӘРТІБІМ Мен сағат 7 00–де тұрамын. Таңертеңгі тамақ ішемін. Сабақ сағат 8 30-да басталады. Үйге сағат 14 00-де келемін. Бір сағат демаламын. Сағат 15 00-ден 18 00-ге дейін сабақ оқимын. ... Сағат 22 00 -де ұйықтаймын.
-
Предмет:
Қазақ тiлi -
Автор:
nichols - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Рассказ на тему как я укрепляю нервную систему
-
Предмет:
ОБЖ -
Автор:
biscuitnggy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
А) 924 и 396
Б) 795 и 1188
В) 495 и 825
-
Предмет:
Математика -
Автор:
phoenix100 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Числа - двести тридцать семь тысяч пятнадцать, Четыреста пять тысяч тридцать четыре, Сто шесть тысяч сто три, Пятьдесять пять тысяч триста сорок семь. Класс тысяч. Разряды. Сотни. Деятки. Единицы. / Класс единиц. Разряды. Сотни. Десятки. Единицы. Ч сло
-
Предмет:
Математика -
Автор:
doogieparks - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years