Задать вопрос Регистрация
Помочь другим

  • lim n⇒∞ 3^n [2*3^2 +3/2(2/3)^n]/3^n[1/3+7*2(2/3)^n]

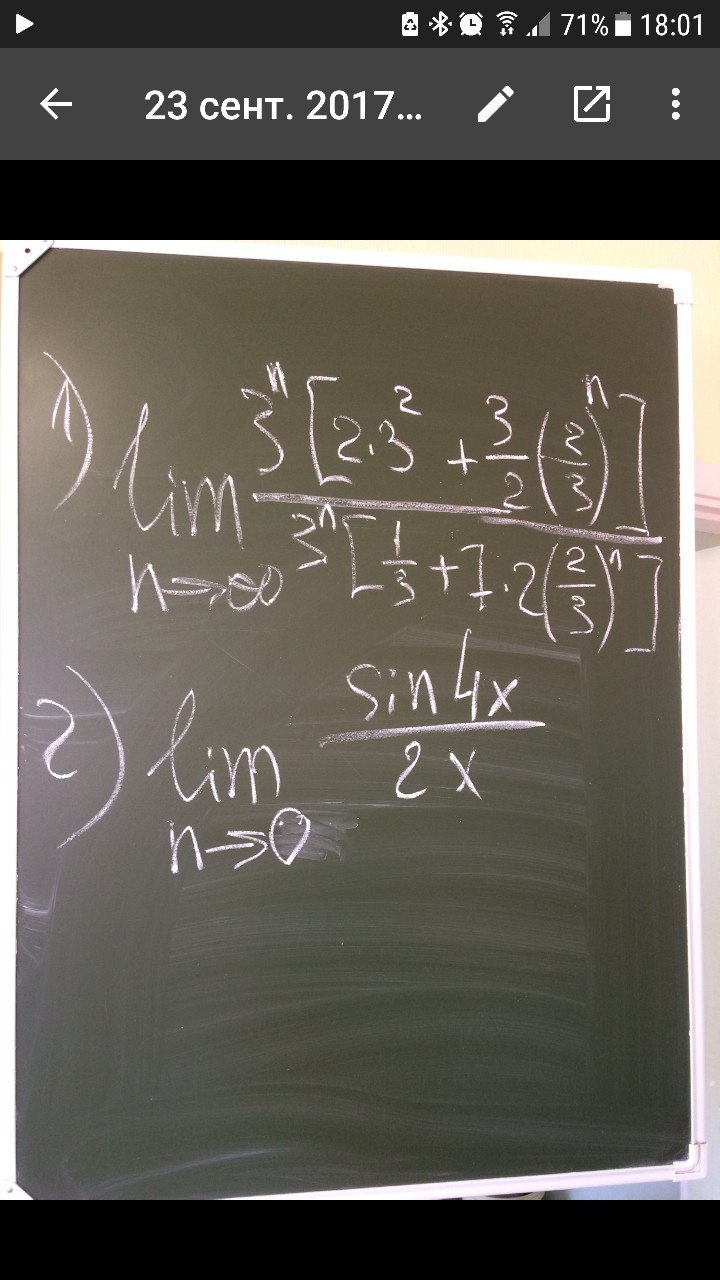
    question img

Ответы 6

  • сё легко

    • Автор:

      ashlee
    • 5 лет назад
    • 0
  • видно
  • если бы не правила сайта я бы тебе просто ответ бы написал

    • Автор:

      probo
    • 5 лет назад
    • 0
  • )))

    • Автор:

      roy13
    • 5 лет назад
    • 0
  • ахахахаха так ладно успокойтесь всё правильно
  • \lim_{n \to \infty} \frac{3^n(2*3^2+ \frac{2}{3}( \frac{2}{3} )^n )}{3^n( \frac{1}{3}+7*2( \frac{2}{3} )^n )} = \frac{ \lim_{n \to \infty} 2*3^2+ \frac{2}{3}( \frac{2}{3} )^n }{ \lim_{n \to \infty} \frac{1}{3}+7*2( \frac{2}{3} )^n }= \frac{ \lim_{n \to \infty} 2*3^2+ \lim_{n \to \infty} \frac{2}{3}( \frac{2}{3} )^n }{ \lim_{n \to \infty} \frac{1}{3}+ \lim_{n \to \infty} 7*2( \frac{2}{3} )^n } \\ = \frac{2*9}{ \frac{1}{3} }=18*3=54 \lim_{n \to \ 0} \frac{sin(4x)}{2x} = \frac{4}{2} \lim_{n \to \ 0} \frac{sin(4x)}{4x} = \frac{4 \lim_{n \to \ 0} \frac{sin(4x)}{4x} }{2}= \frac{4}{2}=2

    • Автор:

      bugsythm5
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years