Алгебра, 10 класс. Отмечу лучшим. Нужно решение, задания и ответы прикрепил.

Ответы 2

https://znanija.com/task/25521722 был бы благодарен ещё за это
- Автор:
  michelle
- 5 лет назад
- 0
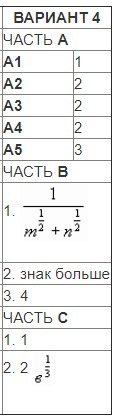
в заданиях A1,A2,A3,A4 используем свойства степени: $a^x*a^y=a^{x+y} \\a^x:a^y=a^{x-y} \\a^{-x}= \frac{1}{a^x} \\(a^{x})^{y}=a^{x*y}$ A1 $\frac{7^{ \frac{7}{3} }*7^{- \frac{4}{3} }}{7^2} =7^{ \frac{7}{3} - \frac{4}{3} -2}=7^{ 1-2}=7^{-1}= \frac{1}{7}$ Ответ: 1A2 $3^{2(1+\sqrt{3})+1-\sqrt{3}-2-\sqrt{3}}=3^{2+1-2}=3^1=3$ Ответ: 2A3 $(b^{\sqrt{3}})^{\sqrt{3}}:b^2=b^{(\sqrt{3})^2-2}=b^{3-2}=b$ Ответ: 2A4 $2^{7-3x}= (\frac{1}{2} )^{x-4} \\2^{7-3x}=2^{-(x-4)} \\7-3x=-x+4 \\3x-x=7-4 \\2x=3 \\x= \frac{3}{2}$ Ответ: 2A5Здесь будем использовать свойство бесконечно убывающей геометрической прогрессиипредставим эту дробь как:0,248+0,000248+0,0000002480,248+0,001*0,248+0,001*0,001*0,248в итоге получим геометрическую прогрессию с первым членом равным 0,248 и знаменателем 0,001формула суммы для бесконечно убывающей геометрической прогрессии: $S= \frac{b_1}{1-q}$ $b_1=0,248 \\q=0,001 \\S= \frac{0,248}{1-0,001} = \frac{0,248}{0,999} = \frac{248}{999}$ Ответ: 3
- Автор:
  kristopherblake
- 5 лет назад
- 0
Добавить свой ответ