-
Найти область значений функции (значения, которые может принимать y).
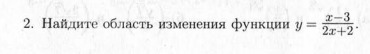
Ответы 1
-
· 1 способ:Преобразуем исходное выражение:
Эта функция - обратная пропорциональность. График получатся смещением графика функции
на 1 влево и на 1/2 вверх.График не пересекает прямую у = 1/2, значит множество значений функции Е(у) = (- ∞ ; 1/2) ∪ ( 1/2 ; +∞)2 способ.Выразим из уравнения х через у:(2x + 2) · y = x - 32xy + 2y - x = - 3x(2y - 1) = - 2y - 3x = (- 2y - 3) / (2y - 1)А теперь найдем область определения этой зависимости х от у:2y - 1 ≠ 02y ≠ 1y ≠ 1/2Е(у) = (- ∞ ; 1/2) ∪ ( 1/2 ; +∞)
-
Автор:
sophierichardson - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
эссе на тему "Величие народа вовсе не исчисляется его численностью , как величие человека не измеряется его ростом. Помогите пожалуйста!!!!!!!
-
Предмет:
Обществознание -
Автор:
crane - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
о чем желеет Марфа Игнатевна?? и пьесы Гроза
СССССРРРРООООЧЧЧЧЧННННОООО-
Предмет:
Литература -
Автор:
skipperk1o7 - 5 лет назад
-
Ответов:
6 -
Смотреть
-
-
объясните причину денежной реформы 16го века
-
Предмет:
История -
Автор:
dayanacurry - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Краткая запись нужна. Упаковщица уложила в коробку 2 ряда желтых кубиков ,по 8 кубиков в ряду, и 16 красных кубиков. Сколько всего кубиков. Краткая запись нужна-
Предмет:
Математика -
Автор:
jj - 5 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
