Задать вопрос Регистрация
Помочь другим

  • Решите неравенство:
    См. прикрепленное изображение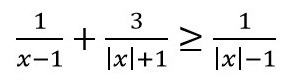

    question img

Ответы 1

  • Область определения: x ≠ 1; x ≠ -1При x < 0 будет |x| = -x \frac{1}{x-1}+ \frac{3}{-x+1} \geq \frac{1}{-x-1} \frac{1}{x-1}- \frac{3}{x-1}- \frac{1}{-x-1} = \frac{-2}{x-1} + \frac{1}{x+1} \geq 0 \frac{-2(x+1)+(x-1)}{(x-1)(x+1)} = \frac{-x-3}{(x-1)(x+1)} \geq 0По методу интерваловx ∈ (-oo; -3] U (-1; 1)Так как по условию x < 0, то решение: x ∈ (-oo; -3] U (-1; 0)При x >= 0 будет |x| = x\frac{1}{x-1}+ \frac{3}{x+1} \geq \frac{1}{x-1} \frac{3}{x+1} \geq 0По методу интерваловx ∈ (-1; +oo)Так как по условию x >= 0, то решение: x ∈ [0; +oo)Общее решение: x ∈ (-oo; -3] U (-1; 0) U [0; +oo)Два интервала можно объединить.Ответ: x ∈ (-oo; -3] U (-1; +oo)

    • Автор:

      lulu89
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years