Задать вопрос Регистрация
Помочь другим

  • Записать систему линейных уравнений, соответствующую уравнению в матричной форме: A*X=B, где X=(x y z) в столбик.
    Решить полученную систему методом Крамера. матрицы обведены в таблице(см картинку)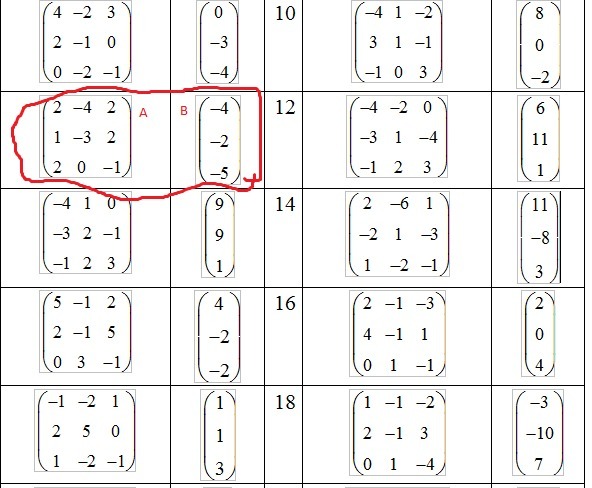

    question img

Ответы 6

  • здесь немножко подправил, посмотрите

    • Автор:

      henry959
    • 5 лет назад
    • 0
  • да ничего страшного, все равно я не списываю не проверив вычисления)))
  • спасибо вам огромное

    • Автор:

      dingo7uga
    • 5 лет назад
    • 0
  • я просто сомневаюсь в своих решениях

    • Автор:

      ace18
    • 5 лет назад
    • 0
  • если можете, решите еще задание
  • \begin{cases}2x-4y+2z=-4,\\ x-3y+2z=-2,\\ 2x-z=-5;\end{cases}\quad \Delta=\,\,\left|\begin{matrix}2 & -4 & 2\\1 & -3 & 2\\2 & 0 & -1\end{matrix}ight|=\left|\begin{matrix}2 & 4 & -2\\1 & 3 & -2\\2 & 0 & 1\end{matrix}ight|=\\ =\left|\begin{matrix}6 & 4 & -2\\5 & 3 & -2\\0 & 0 & 1\end{matrix}ight|=\left|\begin{matrix}6 & 4 \\5 & 3\end{matrix}ight|=18-20=-2.\Delta_1=\,\,\left|\begin{matrix}-4 & -4 & 2\\-2 & -3 & 2\\-5 & 0 & -1\end{matrix}ight|=\left|\begin{matrix}-4 & 4 & -2\\-2 & 3 & -2\\-5 & 0 & 1\end{matrix}ight|=\left|\begin{matrix}-14 & 4 & -2\\-12 & 3 & -2\\0 & 0 & 1\end{matrix}ight|=\\ =\left|\begin{matrix}-14 & 4\\-12 & 3\end{matrix}ight|=-42+48=6;\Delta_2=\,\,\left|\begin{matrix}2 & -4 & 2\\1 & -2 & 2\\2 & -5 & -1\end{matrix}ight|=\left|\begin{matrix}6 & -14 & 0\\5 & -12 & 0\\2 & -5 & -1\end{matrix}ight|=-\left|\begin{matrix}6 & -14\\5 & -12\end{matrix}ight|=\\ =72-70=2;\Delta_3=\,\,\left|\begin{matrix}2 & -4 & -4\\1 & -3 & -2\\2 & 0 & -5\end{matrix}ight|=\left|\begin{matrix}0 & 2 & 0\\1 & -3 & -2\\0 & 6 & -1\end{matrix}ight|=-\left|\begin{matrix}2 & 0\\6 & -1\end{matrix}ight|=2.x=\frac{\Delta_1}{\Delta}=\frac{6}{-2}=-3;\,y=\frac{\Delta_2}{\Delta}=\frac{2}{-2}=-1;\,\,z=\frac{\Delta_3}{\Delta}=\frac{2}{-2}=-1.

    • Автор:

      wood
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years