-
Показательное неравенство!Кто спец? Помогите, пожалуйста, решить!!!! №9
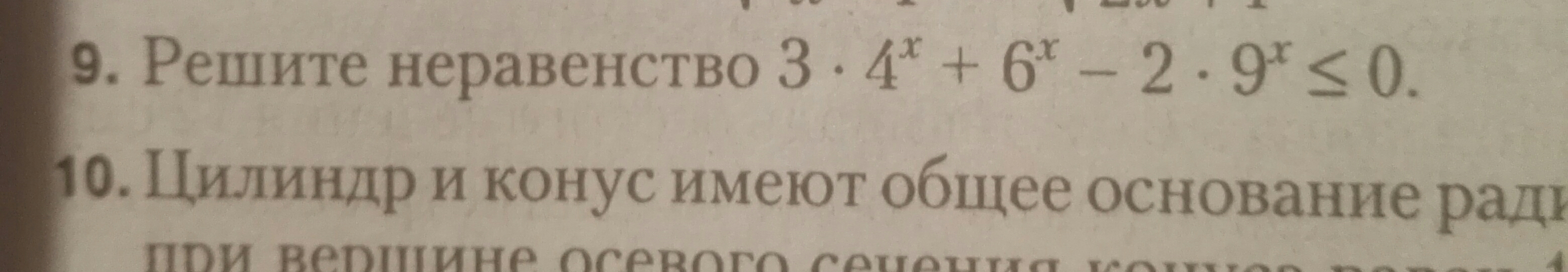
-
Предмет:
Алгебра -
Автор:
elsiedurham - 6 лет назад
-
Ответы 1
-
Имеем:
Преобразуем:
Разделим неравенство на
. Т.к. оно больше нуля, то знак неравенства не изменится:
Пусть
, тогда
Умножим неравеество на t > 0, получим:
Решением данного неравенства является интервал: t ∈ [-1; 2/3]Однако с учётом того, что t не меньше нуля: t ∈ [0; 2/3]Делаем обратную замену:
Данное неравенство может выполняться только при x ≥ 1
-
Автор:
jaxsonbrock - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
найти обьем 44 г углекислого газа и количество вещества
-
Предмет:
Химия -
Автор:
dreameyfoxk - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Что такое склонение?
И что такое 2-ое склонение?-
Предмет:
Русский язык -
Автор:
cooperhwdo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
яка протяжність африки у кілометрах на карті
-
Предмет:
География -
Автор:
parkerisew - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дано: катеты MP и PK прямоугольного треугольника MPK соответственно равны 24 см и 10 см
Найти : длины проекций на гипотенузу.
Помогите пж!-
Предмет:
Геометрия -
Автор:
queenfarley - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
