-
Решить тригонометрическое уравнение ( а) и найти его корни, принадлежащие отрезку (б)
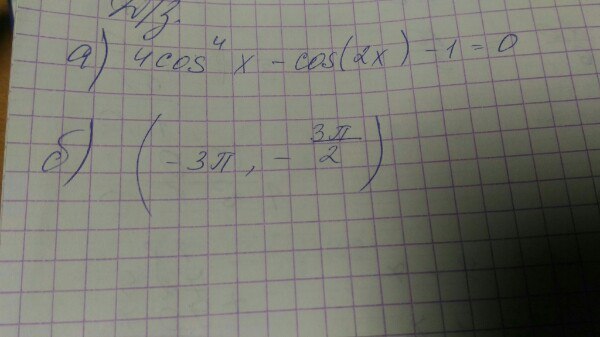
Ответы 2
-
Спасибо за исправление)
-
Автор:
alfonsoharris - 6 лет назад
-
0
-
-
task/25729079--------------------( а) Решить тригонометрическое уравнение 4cos⁴x -cos(2x) -1 =0 и (б) найти его корни, принадлежащие интервалу ( -3π ; -3π/2) .-----------------(a)(4cos⁴x -1) -cos(2x) =0 ; * * * (2cos²x)² -1²) -cos(2x) =0 * * *(2cos²x -1)(2cos²x +1) - cos(2x) =0 ;cos(2x) (2cos²x +1) - cos(2x) =0 ;cos(2x) (2cos²x +1-1) =0 ; 2cos²x * cos(2x) =0 ; * * * [ cos²x =0 ; cos(2x) =0. * * * 1) cosx =0 ⇒ x₁ =π/2 +πk , k ∈ Z ;2) cos(2x) =0 ⇒ 2x =π/2 +πk , k ∈ Z ⇔ x₂ =π/4 + (π/2)*k , k ∈ Z. ответ: x₁= π/2 +πk ; x₂ = π/4 + (π/2)*k , k ∈ Z. =====================================(б) x₁= π/2 +πk только при k = - 3 x = - 5π/2 ----x₂ = π/4 + (π/2)*k -3π < π/4 + (π/2)*k < -3π /2 ⇔ -6π < π/2 +πk < -3π⇔ -6,5π <πk< -3,5π⇔-6,5 < k < -3,5 , т.е . - 6 ≤ k ≤ - 4 k _целое : - 6 ; -5 ; - 4-11π/4 ; - 9π/4 ; - 7π/4 .ответ: -11π/4 ; - 5π/2 ; - 9π/4 ; - 7π/4.
-
Автор:
libbyrosales - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какая мораль в басни Измайлова (Филин и Чиж)?
-
Предмет:
Литература -
Автор:
twixxrbl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
о чем 4 5 6 главы романа Дубровский?! Срочно надо до завтра даю 40 баллов
-
Предмет:
Литература -
Автор:
miguelhenderson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Среди принятых в школу только 20чел умеют читать писать и считать .Тех кто не знает грамоты в 5р больше а остальные не знакомы с арифметикой Сколько надо обучить грамоте и сколько арифметике
-
Предмет:
Математика -
Автор:
ernie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
укажите основной признак прчного централизованного государства
-
Предмет:
Қазақ тiлi -
Автор:
maddiesvkh - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
