-
Докажите, что при любом n∈Z является целым числом значение выражения:
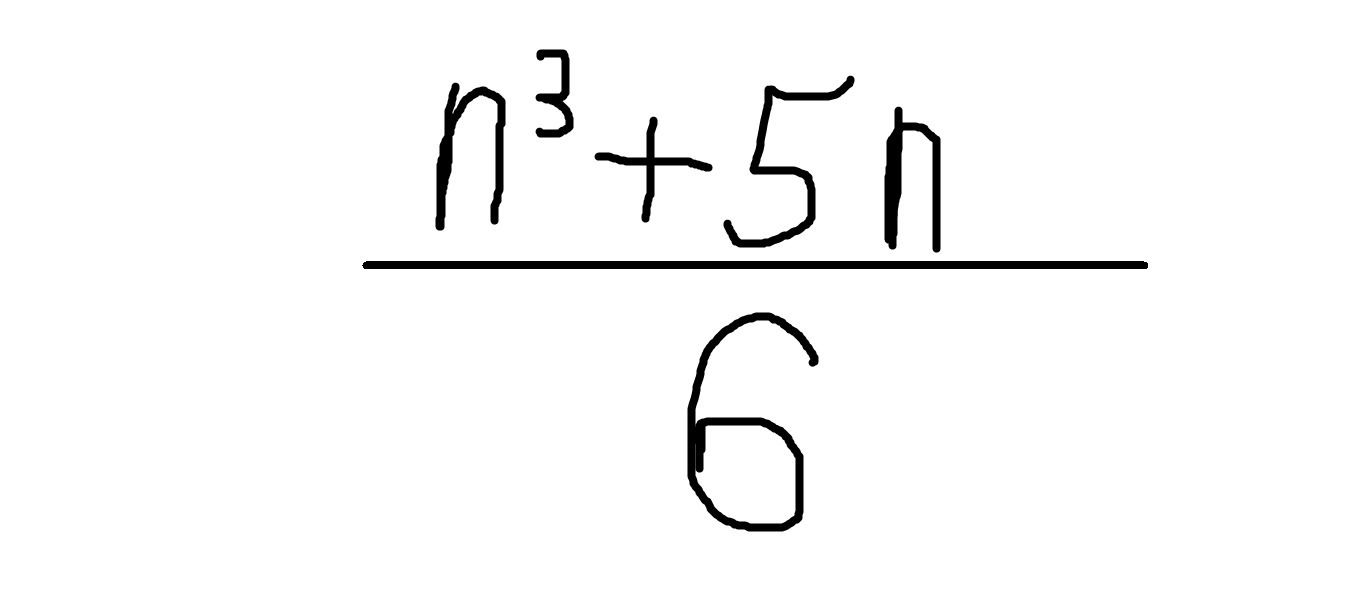
-
Предмет:
Алгебра -
Автор:
waylonxjor - 5 лет назад
-
Ответы 1
-
Достаточно доказать что
делиться на 6 при любом целом n. Для n=0 утверждение очевидно.Докажем по индукции: Если n > 0, то
. Для n=1 утверждение верно. Предположим что утверждение верно для некоторого n > 1. Докажем утверждение для (n+1).
Достаточно доказать что
делиться на 2. ======================================================================Лемма:Для всех натуральных n, число
делиться на 2.Доказательство: Для n=1 утверждение очевидно. Предположим что утверждение верно для некоторого n>1. Докажем для (n+1):
Следуя предположению, первое слагаемое делиться на 2. Следовательно и всё выражение делиться на 2. Отсюда следует что для всех натуральных n, число
делиться на 2.======================================================================Первое слагаемое делиться на 6 следуя предположению, второе слагаемое делиться на 3 и на 2 (следуя лемме), т.е. делиться на 6. Откуда и получаем что всё выражение делиться на 6. Следовательно, для всех n > 0 натуральных, данное выражение делиться на 6.Если n < 0 то
, однако мы уже доказали для всех натуральных, что данное выражение делиться на 6. Откуда следует, что всегда существует такое натуральное число t, так что:
.Т.е. утверждение верно и для отрицательных чисел. Ч.Т.Д.
-
Автор:
venanciosaunders - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
КАКОЕ ПРОВЕРОЧНОЕ СЛОВО К СЛОВУ ПРАЗДНИК НЕПРОИЗНОСИМАЯ СОГЛАСНАЯ Д
-
Предмет:
Русский язык -
Автор:
hebert - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- область определения y=log3 (2x-1)
-
45 конфет стоят столько же рублей сколько их можно купить на 20 рублей.сколько конфет можно купить на 5 рублей
-
Предмет:
Математика -
Автор:
aimeev4yw - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какие параметры используются в приборах с параметрическим ВТП для выделения полезной информации?
How much to ban the user?
1 hour
1 day
100 years
