-
Пожалуйста, решите !!!! Очень нужна помощь! Очень прошу! Если можно с решением! Срочно !!!!!!
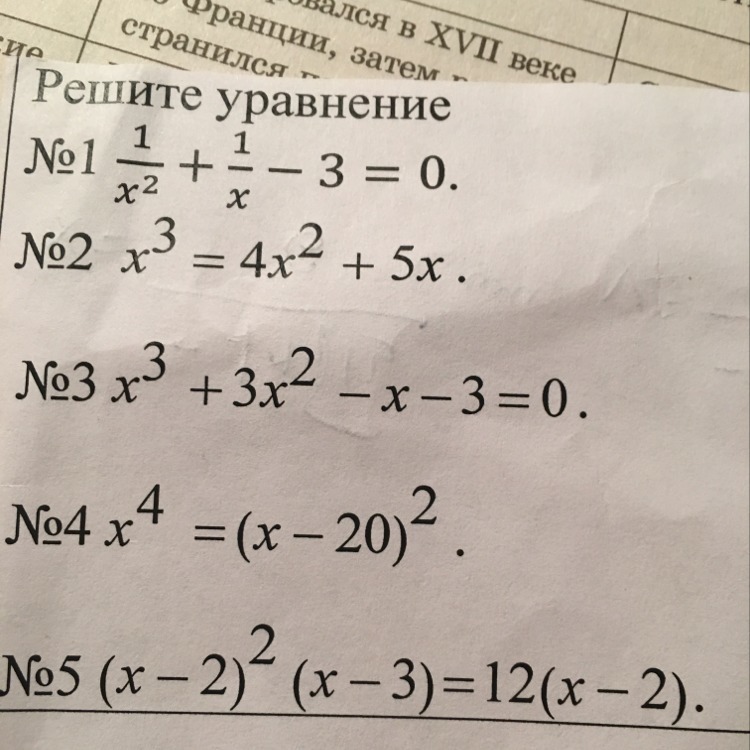
Ответы 1
-
N1. Домножаем уравнение на х², х=0 не является корнем уравнения. Получаем-3х²+х+1=03х²-х-1=0D=1²+4*3=13√D=√13х₁=(1-√13)/6х₂=(1+√13)/6N2 x³=4x²+5xx³-4x²-5x=0x(x²-4x-5)=0Один ответ х=0х²-4x-5=0D=4²+4*5=16+20=36√D=6x₁=(4-6)/2=-1x₂=(4+6)/2=5Ответ: три корня -1, 0 и 5N3. x³+3x²-x-3=x³-x+3x²-3=x(x²-1)+3(x²-1)=(x+3)(x²-1)=(x+3)(x-1)(x+1)Получаем(x+3)(x-1)(x+1)=0Ответ: три корня х₁=-3, х₂=-1, х₃=1N4 x⁴=(x-20)²Берем квадратный корень из обеих частей равенства. Получаем x²=+-(x-20)Два варианта:1. x²=(x-20)x²-x+20=0D=1²-4*20=1-80=-79. Решения нет2. x²=-(x-20)x²+x-20=0D=1²+4*320=1+80=81√D=9x₁=(-1-9)/2=-5x₂=(-1+9)/2=4Ответ: два корня-5 и 4N5. (x-2)²(x-3)=12(x-2)1. Первый корень когда х-2=0, х=22. Если х-2≠0, то на (х-2)можно сократить. Получаем (x-2)(x-3)=12x²-3x-2x+6=12x²-5x+6-12=0x²-5x-6=0D=5²+4*6=25+24=49√D=7x₁=(5-7)/2=-1x₂=(5+7)/2=6Ответ: три корня -1, 2 и 6
-
Автор:
einsteinqibh - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Что такое политическая карта природа 4класс
-
Предмет:
Окружающий мир -
Автор:
urielgross - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Производные 2*х-√х+6х*3
-
Предмет:
Математика -
Автор:
guzman - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
почему книгу называют источником знаний.написать сочинение..
-
Предмет:
Другие предметы -
Автор:
cristinabond - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
как разобрать слово домик по составу?
-
Предмет:
Русский язык -
Автор:
linnea - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
