-
докажите торжество
arctg(1/2)+arcctg(1/3)=pi/4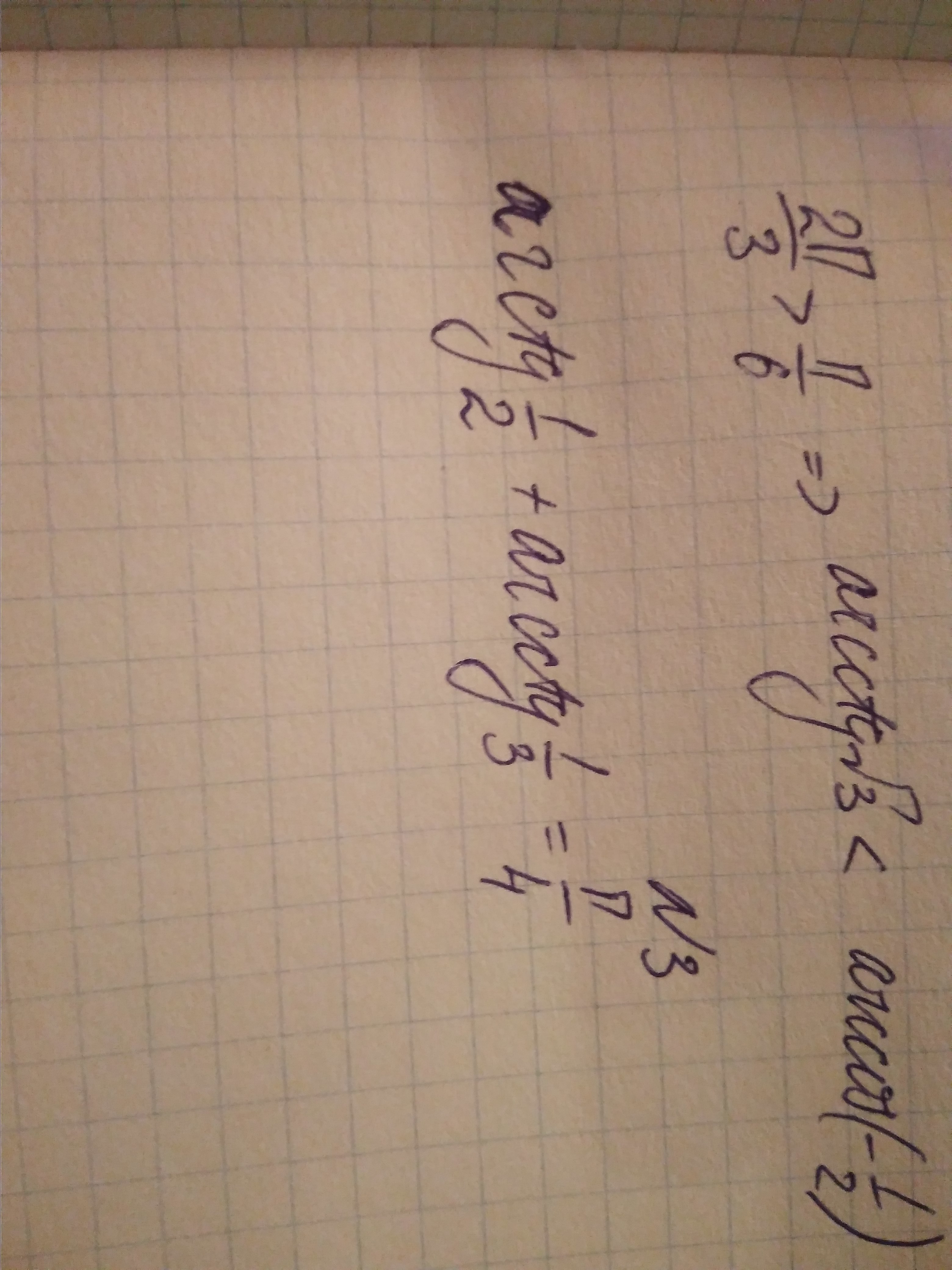
-
Предмет:
Алгебра -
Автор:
bernicepnhk - 5 лет назад
-
Ответы 1
-
task/26323516--------------------Докажите тождество :arctg(1/2) + arcctg(1/3) = π /4 --------------------- Пусть arctg(1/2) + arcctg(1/3)= φ * * * tg(α + β) = ( tgα + tgβ) / (1 -tgα *tgβ ) * * *tgφ = tg( arctg1/2 + arcctg1/3 ) =tg( arctg1/2 + arctg3 )( tg( arctg1/2) +tg( arctg3) ) / (1 - tg( arctg1/2) *tg( arcctg3 ) ) == (1/2 +3) /(1 -(1/2)*3) =3,5 /(-0,5) = - 7 . φ ≠ π/4 ⇒ пример неверно .========================================Верное тождество : arctg(1/2) + arctg(1/3) = π /4 . φ = arctg1/2 + arctg1/3 tgφ = tg( arctg1/2 + arctg1/3 ) =( tg( arctg1/2 +tg( arctg1/3 ) / (1 -tg( arctg1/2) *tg( arctg1/3 ) ) == (1/2 +1/3) / ( 1 -(1/2)*(1/3) ) = (5 /6 ) / (5/6) = 1 . ⇒ φ = π/4 .
-
Автор:
brunowalls - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Вставь пропущенные буквы,выдели окончания,укажите спряжение глаголов:
Вызов...шь врача, выпь...шь кофе, выль...т воду, Вася напил...т и накол...т дров, ты не обид...шь младшего брата, почин...т велосипед, постро...шь домик, выпол...шь огород, расстел...шь скатерть, вынес...шь мусор, вымо...шь пол, удвид...шь друга.-
Предмет:
Русский язык -
Автор:
heraclio - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Сообщение на тему скульптура России
-
Предмет:
Обществознание -
Автор:
felix30 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
ПОЖАЛУЙСТА ПОМОГИТЕ , ОЧЕНЬ СРОЧНО
На оси ординат найдите точку С, равноудаленную от точек А (4; −3) и В (8; 1). -
Интересную игру
Какой род и падеж?-
Предмет:
Русский язык -
Автор:
francescayates - 5 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
