-
Укажите все значения х при которых имеет смысл выражение
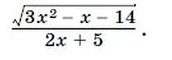
-
Предмет:
Алгебра -
Автор:
valerianob9xj - 5 лет назад
-
Ответы 3
-
Внимательно следи за тем, где круглые скобки, а где квадратные
-
Автор:
walterrojas - 5 лет назад
-
0
-
-
спасибооо
-
Автор:
winters - 5 лет назад
-
0
-
-
Во первых подкоренное выражение корня чётной степени должно быть ≥ 03x² - x - 14 ≥ 0Найдём корни, приравняв квадратный трёхчлен к нулю:3x² - x - 14= 0D = (-1)² - 4*3*(-14) = 1 + 168 = 169X₁ = (1 + √169)/6 = (1 + 13)/6= 14/6 = 2 2/3X₂ = (1 - √169)/6= ( 1 - 13)/6 = - 12/6 = - 23(x - 2 2/3)(x + 2) ≥ 0(x - 2 2/3 )(x + 2) ≥ 0 + - +________________________________ - 2 2 2/3x ∈ (- ∞ ; - 2]∪[2 2/3 ; + ∞)Во вторых знаменатель дроби не должен равняться нулю:2x + 5 ≠ 02x ≠ - 5x ≠ - 2,5Объединим эти два условия и выпишем окончательный ответ:\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ ///////////////////////////___________₀__________________________________ - 2,5 - 2 2 2/3x ∈ (- ∞ ; - 2,5)∪(- 2,5 ; - 2]∪[2 2/3 ; + ∞)
-
Автор:
kasonyork - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Переведите из двоичной системы в десятичную101001011
-
Предмет:
Информатика -
Автор:
basil - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите пожайлуста сейчас по окружающему миру на тему экологические проблемы и охрана природы в лесных зонах кратко
-
Предмет:
Окружающий мир -
Автор:
tarynwksz - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Реши задачу:
Больному прописали лекарства, которые нужно пить по 2 таблетки 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства. Какого наименьшего количество упаковок на весь курс лечения?
Пожалуйста помогите!-
Предмет:
Математика -
Автор:
galvan - 5 лет назад
-
Ответов:
4 -
Смотреть
-
-
1.Запишите 5 слов , с непарными твердыми согласными
2. Запишите 5 слов , с непарными мягкими согласными-
Предмет:
Русский язык -
Автор:
stacymeadows - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
