-
Степень с рациональным показателем
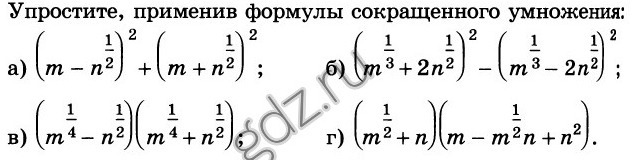
-
Предмет:
Алгебра -
Автор:
gwendolen9ohr - 5 лет назад
-
Ответы 4
Еще вопросы
-
Просклоняйте слово "молодёжь" по склонениям
1 склонение; Род: Мужской, Женский; Окончание: а, я
2 склонение; Род: Средний, Мужской; Окончание: е, о, нулевое
3 склонение; Род: Женский; Окончание: нулевое (ь)-
Предмет:
Русский язык -
Автор:
alejandra55 - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
помогите решить,по теореме Виета
x^2-7x+2=0
x^2-это икс во второй степени(если кто-то не знает)-
Предмет:
Алгебра -
Автор:
gloriaberry - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Выразите время. в минутах 2 ч 16 мин, 8 ч 1 мин, 10 ч; в секундах 9 мин, 6 мин, 3 мин 58 сек, 4 мин 1 сек. помогите пожалуйста
-
Предмет:
Русский язык -
Автор:
savannahsanchez - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
решить х+(-5)=2 уровнение
-
Предмет:
Математика -
Автор:
kismetlrfo - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years

