Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста!!
    Нужно найти производную этой функции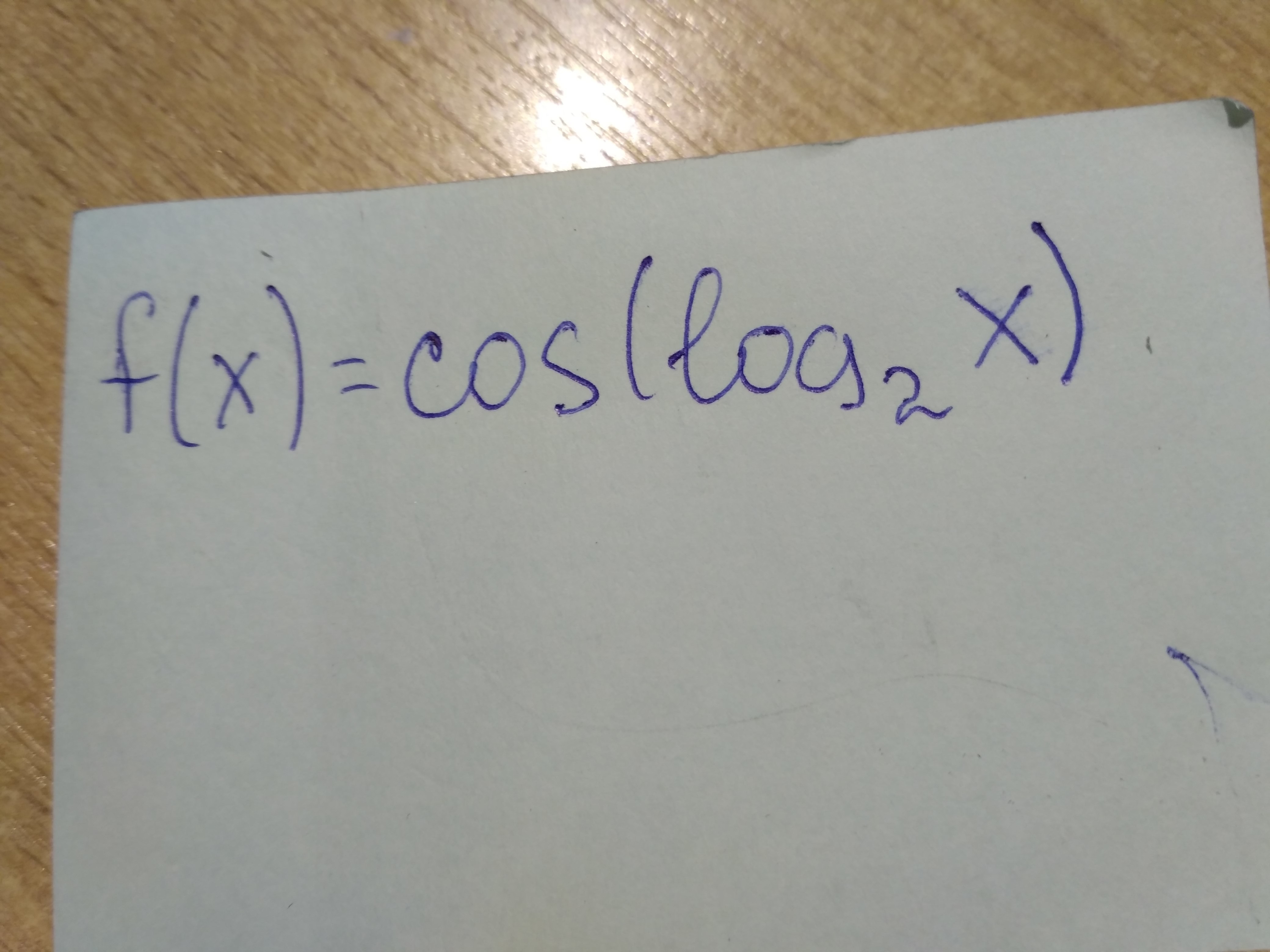

    question img

Ответы 2

  • большое спасибо)
  • Вначале, для удобства, найдем производные следующих функций:\displaystyle (\cos t)' =-\sin t\\\\ (\log_2 x)'=\left( \frac{\ln x}{\ln 2}ight) '= \frac{ \frac{1}{x} \cdot \ln 2}{(\ln 2)^2} = \frac{1}{x\ln 2} Теперь, следуя Цепному правилу, получаем:\displaystyle f'(x)=\cos '(\log_2 x) \cdot (\log_2 x)' = -\sin(\log_2 x) \cdot \frac{1}{x\ln 2} = - \frac{\sin(\log_2 x)}{x \ln 2}

    • Автор:

      eileen
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years