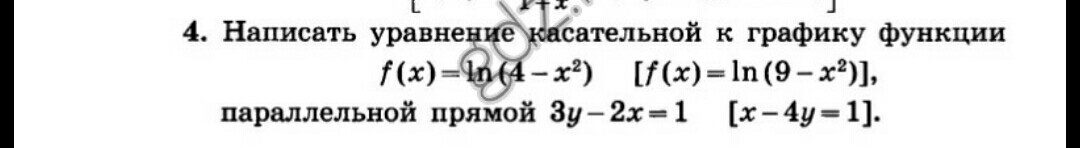Ответы 5
-
спасибо вам онромное
-
Автор:
ann89 - 5 лет назад
-
0
-
-
огромное*
-
Автор:
heidihopkins - 5 лет назад
-
0
-
-
2x² -6x -8 = 0 , x₁ ≠ 8
-
Автор:
mohamedshaffer - 5 лет назад
-
0
-
-
1) написать уравнение касательной.
и параллельной
Нам не дана точка касания.. Но это не проблемаПараллельность прямых означает равенство к-тов k (y=kx+b)и т-нт k это значение производной в точке касаниянайдем производную
приравняв ее значение 2/3 мы найдем точку касания
вроде бы получили две точки.. но не забываем проверить ОДЗ(4-х²)>0; x²<4; -2<x<2Так что у нас только одна точка х=-1Теперь составим уравнение касательной
2) не так подробно
х=9 опять же не лежит в ОДЗтогда точка касания х=-1
-
Автор:
larry89 - 5 лет назад
-
0
-
-
task/26672000---------------------см приложение

-
Автор:
mercedes50 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите пожалуйста беларусский язык 3 класс 1 часть упр. 209
-
Предмет:
Беларуская мова -
Автор:
beau88 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- Мать и мачеха классификации
-
решить уравнение 2/х=8/5
-
Предмет:
Математика -
Автор:
luna35 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
придумать современную сказку Что нужно для счастья
-
Предмет:
Русский язык -
Автор:
sharonwiggins - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years