-
Докажите, что число рациональное:
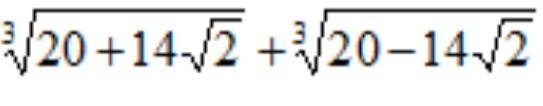
-
Предмет:
Алгебра -
Автор:
desiree4jab - 5 лет назад
-
Ответы 1
-
\sqrt[3]{20+14 \sqrt{2} }+ \sqrt[3]{20-14 \sqrt{2} }= \\ = \sqrt[3]{8+12 \sqrt{2}+12+2 \sqrt{2} }+ \sqrt[3]{8-12 \sqrt{2}+12-2 \sqrt{2} }= \\ = \sqrt[3]{(2+ \sqrt{2})^3 }+ \sqrt[3]{(2- \sqrt{2})^3 } = \\ =2+ \sqrt{2}+2- \sqrt{2}= \\ =4 Доказано.Применялись формулы сокращенного умноженияКуб суммыa^3+3a^2b+3ab^2+b^3=(a+b)^3Куб разностиa^3-3a^2b+3ab^2-b^3=(a-b)^3
-
Автор:
hunterm5u8 - 2 года назад
-
2
-
-
Добавить свой ответ
Еще вопросы
-
Как читать? Пропись номер 3 Андриановой стр 7. 1 класс, Россия.
-
Предмет:
Другие предметы -
Автор:
duke10 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- битва решившая судьбу Англии при завоевании её Норманнами в 1066 году произошла.... (где?)......
-
Речення на слова вісті,свято,камінці,свято,цвях,гості.
-
Предмет:
Українська мова -
Автор:
gisela - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста составить 5 предложений синтоксических ролей слова: Россия
-
Предмет:
Русский язык -
Автор:
lilyanamyi4 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
